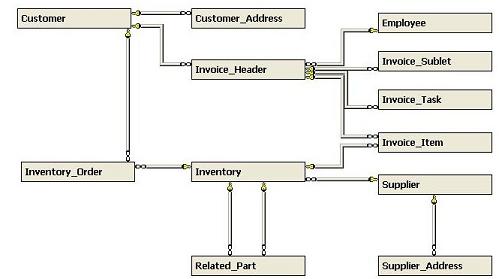
When merging two databases with the same schema, primary keys may have the same values in both databases, yet represent unrelated records. Typically you would carry over such keys as legacy values, re-create new ones in the target database, and then re-calculate all foreign keys that reference them in related tables. But in what order should these tables be ported to avoid violating referential integrity in the target database? Consider the following schema for a customer database (Fig. 1):
If this database is appended to another database having the same schema, all primary keys in the source database must be re-calculated to new values in the target database to avoid clashing with existing values. Furthermore, all foreign keys pointing to them from other tables must also be re-calculated so they continue referencing the same records as before. That's the easy part.
The hard part is figuring out the order these tables should be ported.
In the example above, the Customer table must be ported before the Customer_Address table so that referential integrity won't be violated in the target database. In other words, when porting the latter table, all records from the former table must already be present so that the foreign key in the latter table can be re-calculated using the legacy values from the original table. Otherwise the insertions will fail.
We want to assign a "level" to each table, so that if they're ported by ascending level then no violations of referential integrity will occur. In the above example, it's easy to see that the following assignment of levels will do that:
| Level | Table | Abbreviation |
| 0 | Customer | C |
| 0 | Employee | E |
| 0 | Supplier | S |
| 1 | Customer_Address | CA | 1 | Invoice_Header | IH | 1 | Inventory | I | 1 | Supplier_Address | SA | 2 | Inventory_Order | IO | 2 | Invoice_Sublet | IS | 2 | Invoice_Task | IT | 2 | Invoice_Item | II | 2 | Related_Part | RP |
Here the Customer, Employee and Supplier tables may be ported in any order (so long as they're ported first). Ditto for Customer_Address, Invoice_Header, Inventory, and Supplier_Address (so long as they're ported next). But Invoice_Item must be ported later since it has a foreign key pointing to Invoice_Header.
Furthermore, it's easy to see that this assignment of levels is "optimal" in the sense that each table receives the lowest possible assignment.
The following script computes an optimal assignment of levels that preserves referential integrity. To explain how it works, it's helpful to use the language of partially-ordered sets (see http://en.wikipedia.org/wiki/Partially_ordered_set  for an overview of posets).
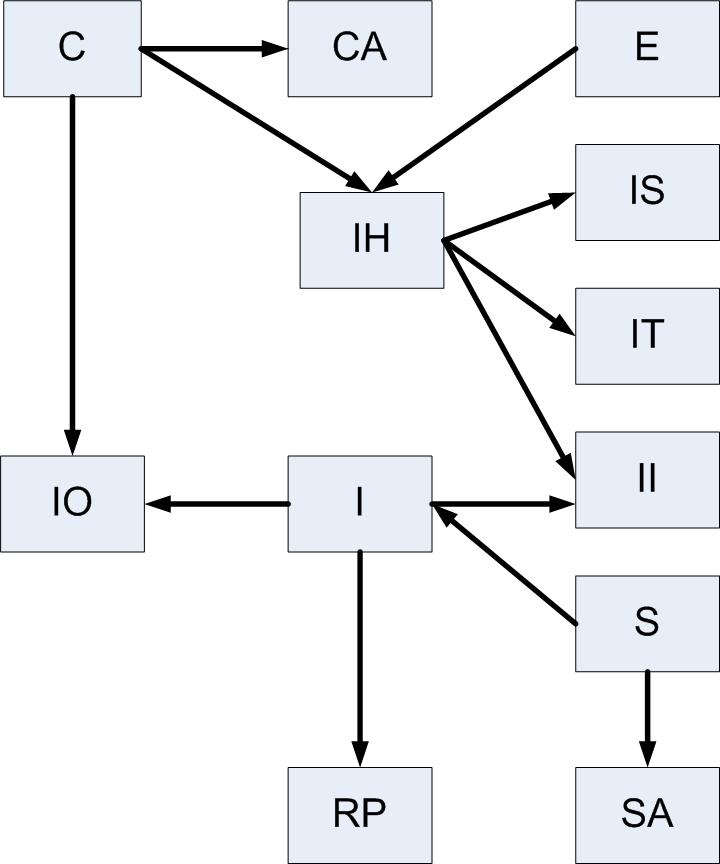
Suppose that Invoice_Header has a foreign key pointing to Customer. We can represent this dependency as:
Customer < Invoice_Header
where the "smaller" table Customer must be ported before Invoice_Header.
Suppose also that Invoice_Item has a pointer to Invoice_Header.
Then Invoice_Header < Invoice_Item.
Of course, this now implies that Customer must always be ported before Invoice_Item even though there's no direct link between them.
To formally describe this "transitivity of dependency", recursively define the relationship << as:
A << B if A < B
A << B if A < C and C << B for some C
Prolog programmers will recognize these "axioms" as the classical ancestor relationship. In particular, Customer << Invoice_Item. More generally, << is a partial order expressing what tables must be ported before others, even if there's no pointer between two tables satisfying this relationship.
It's easy to demonstrate that << defines a partial order since closed loops in < (called a preorder) aren't possible for tables with data in them. Note that two tables violating referential integrity can still co-exist providing that no records have been inserted into either of them (and of course, it will always remain that way). This remote possibility is addressed by the script because otherwise they'll cause infinite loops.
To port these tables while respecting their dependencies, it's sufficient to list them in such a way that each table appears "before" those that are "larger" in the partial ordering <<. That's what the script does. The so-called Hasse diagram in Fig. 2 displays the above preorder (with arrows representing <). It will show us how to assign the table levels.
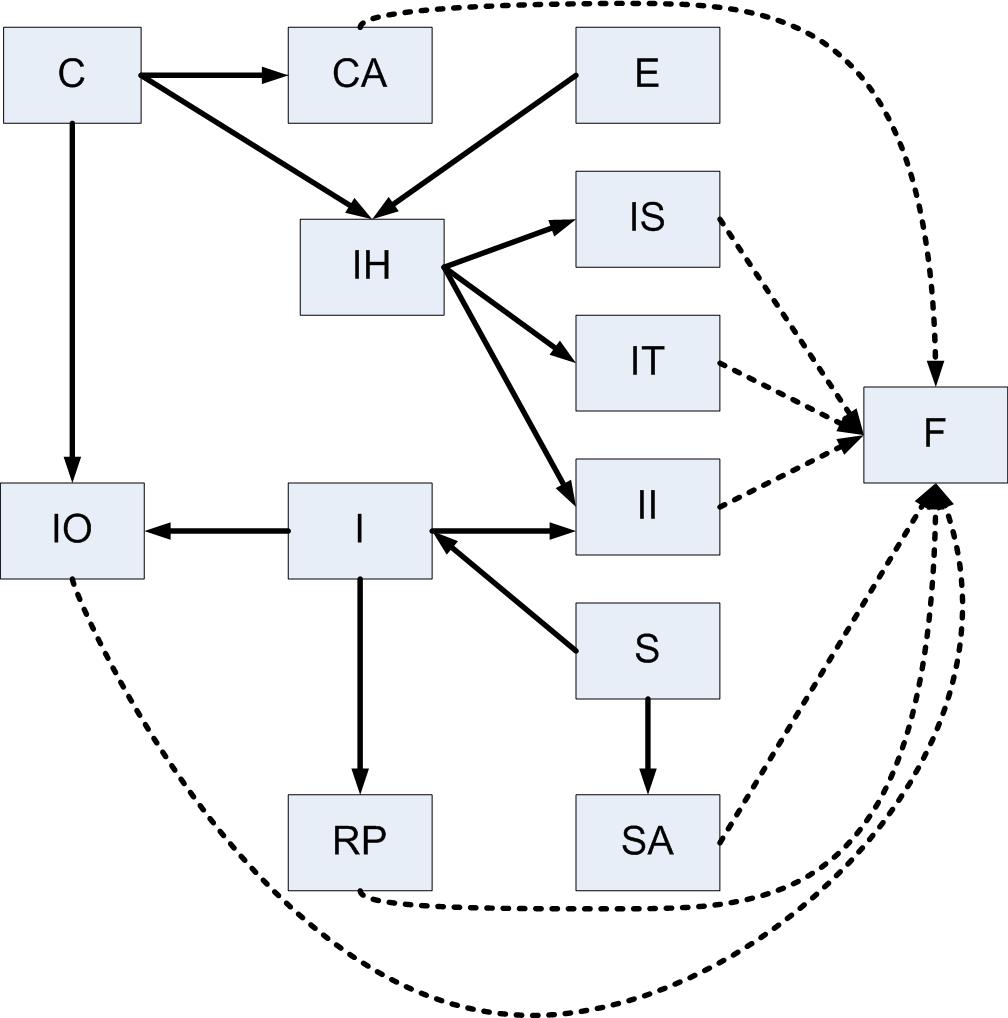
What we first do is add a fictional table F (see Fig. 3) and enough virtual arrows so that every non-fictional table points to at least one other table (possibly fictional). By using this trick we'll avoid special cases. This virtual object is reminiscent of the well-known "point of infinity" in non-Euclidean geometry since its purpose is to simply appear "bigger" than anything else in the database for the purposes of the script.
Then we select those tables to which no arrow points, assign a level of 0 to them, and remove them from the diagram (along with all arrows connected to or from them). These are the tables that can be ported first, since no other tables depend on them.
For example, we would remove S and its two arrows. But since arrows are represented in the script by rows of an SQL Server table whose columns define the "to" and "from" tables, SA would suddenly disappear if the fictional table weren't present (so SA would never be part of the final answer). That's why we have F.
After this we start all over with whatever remains, but assign a level of 1. Note that SA has been assigned a level of 1 at this point, but it could never be assigned anything lower because an incoming arrow was originally present (from S). In particular, each table will be assigned its own level "just in time". In fact, levels are just the longest path lengths of any table to one of level 0, if you follow the arrows backwards. We continue this way until no more elements remain. Then we remove F from the answer.
The script is in the Resources section below
I've used permanent tables to compute the answer (instead of table variables) so readers can verify the computations as the script proceeds (the last two lines will need to be deleted for this). Furthermore, since preorders appear naturally in computing, the script can be used for other purposes where you want to know the level of each object in such relationships (simply replace the snippet that uses SQL Server's sys.foreign_key_columns with one of your own). For the mathematically inclined, this exercise determines the maximum cardinality of ancestor chains for every point in a preorder.
This technique was used to join 17 faculty departments in a major university, where special processing was required on each lookup table (e.g. academic titles) since incompatible values were used before they were merged.