This article is a sequel to "Ordering Tables To Preserve Referential Integrity" which appeared in www.sqlservercentral.com on 20 Mar 2009
Overview
Email broadcasting is nothing more than re-directing emails to multiple addresses, but it’s a common tool for many companies. However, maintaining broadcast lists can be surprisingly difficult. Customers sometimes receive multiple copies of the same email (for no obvious reason) or none at all. A frequent complaint is that recipients ask to be removed from a mailing list but continue to receive them even after the sender attempts manual corrections. This article will show two ways in which subtle errors may occur, and offers a general method for cleaning up broadcast tables using a bit of mathematics and a nice feature of SQL Server 2005.
Although mailing lists are conceptually simple, several people may be independently maintaining them (using private spreadsheets, for example). This can cause many errors. And some of them aren’t even evident until after the re-directions have been collated into a master list (e.g. two people independently putting the same email on their own spreadsheets).
To show how this can happen, take a fictitious company called My Company whose email re-directions look like the following (after Sales, Marketing, and Admin have submitted their re-directions to their email administrator):
bill@MyCompany.com bill@Microsoft.com SALES@MyCompany.com lan@MyCompany.com SALES@MyCompany.com ADMIN@MyCompany.com SALES@MyCompany.com janet@IBM.com SALES@MyCompany.com accounts ADMIN@MyCompany.com accounts sue@MyCompany.com bill@Microsoft.com jane@MyCompany.com webmaster mary@MyCompany.com glen@MyCompany.com glen@MyCompany.com janet@IBM.com natasha@MyCompany.com MARKETING@MyCompany.com lan@MyCompany.com natasha@MyCompany.com fair@MyCompany.com president MARKETING@MyCompany.com fair@MyCompany.com MARKETING@MyCompany.com SALES@MyCompany.com
Here, any email sent to bill@MyCompany.com would be automatically re-directed to bill@Microsoft.com (the parent company). SALES@MyCompany.com is a mailing list whose recipients are lan@MyCompany.com, ADMIN@MyCompany.com (another mailing list), janet@IBM.com, and accounts (a user account on the company’s email server).
Already there are two errors in this broadcast (you did see them, right?):
CIRCULARITY (return to sender):
MARKETING@MyCompany.com -> SALES@MyCompany.com -> lan@MyCompany.com -> natasha@MyCompany.com -> MARKETING@MyCompany.com
REDUNDANCY (recipient occasionally receives multiple copies of the same email):
SALES@MyCompany.com -> accounts
SALES@MyCompany.com -> ADMIN@MyCompany.com -> accounts
The scripts below locate these problems in any email broadcast.
How the scripts work
For notational simplicity, label the email addresses from 1 to 16:
1 bill@MyCompany.com
2 sue@MyCompany.com
3 jane@MyCompany.com
4 mary@MyCompany.com
5 glen@MyCompany.com
6 natasha@MyCompany.com
7 lan@MyCompany.com
8 fair@MyCompany.com
9 MARKETING@MyCompany.com
10 SALES@MyCompany.com
11 ADMIN@MyCompany.com
12 bill@Microsoft.com
13 janet@IBM.com
14 webmaster
15 president
16 accounts
Then the 15 re-directions defining the broadcast look like this:
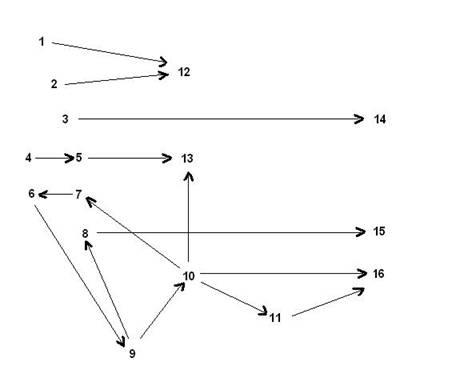
What a difference a picture makes!
Now it’s easy to see why 9 (Marketing) eventually re-directs mail back to itself and why 16 (accounts) always gets multiple emails sent to 10 (SALES). For some reason ADMIN (11) wasn’t aware that SALES was already copying her emails to accounts. For many organizations there could be hundreds of re-directions from a single email, which is why manual tinkering is ineffective.
To diagnose these pictures, let’s view them as directed graphs where the above problems can be approached in a natural way (for an overview of graphs, see http://en.wikipedia.org/wiki/Graph_theory).
Recall that a directed graph is any finite set of elements (called vertices), together with a set of directed edges between them. Multiple edges between any pair of vertices are not permitted, as well as edges involving the same vertex. The scripts below will assume these conditions to keeps things simple. In any event, they’re easy to test.
By definition, for any directed edge A -> B between vertices A and B, the element A is called the LHS (“left-hand side”) and B is called the RHS (“right-hand side”) of the edge.
Lists of re-directions (i.e. single broadcast) will be represented by a table whose columns are LHS and RHS. Later we’ll see why this edge-oriented approach is a natural choice over its vertex-oriented alternative.
For directed graphs, any finite sequence of directed edges V1-> V2-> … -> Vn on the vertices V1, V2, … Vn is called a path (of length n-1), provided that the Vi are distinct (except that V1may be Vn). A path is circular if V1= Vn.
The scripts below will test any broadcast for the following conditions:
· There are no circular paths
· At most one directed path exists between any two vertices
Showing that a directed graph has no circular paths is fairly straightforward.
First, a simple definition. The out-degree of any vertex V is the number of edges of the form V -> W. This is nothing more than the number of edges leading from V to other vertices. In-degrees are defined in the same way.
If the graph has no circular paths, then there must be a vertex V whose out-degree is 0, because the number of vertices is finite.
Our test will attempt to list the vertices in the following way. Choose a vertex whose out-degree is 0 as the first member of the list. Remove it and all edges into it, and repeat for the remaining graph. This process will eventually choose all of the vertices if, and only if, there is no circular path in the original graph (use induction on the number of vertices). Note that if you remove a vertex on the RHS of an edge coming from another vertex with no other edges, then that vertex can also be dropped at this stage because the next iteration will drop it anyway. But since we are storing graphs as edges, this will happen automatically (hence the edge-oriented approach).
For the above example, the vertices with out-degree = 0 are first chosen:
12, 13, 14, 15, 16
After removing these vertices and their edges, the vertices on the remaining graph with out-degree = 0 are chosen:
5, 8, 11
After removing these vertices and their edges, the remaining graph still contains the vertices 9, 10, 7, 6 but none have out-degree = 0. So the test fails, and the remaining graph must have a circular path which, in this case, traverses all of the remaining vertices. Note that if there were three more vertices connected in the following way 17 -> 18 -> 19 -> 17 then there would be two circular paths, but neither would traverse all of the remaining vertices. So this algorithm won’t immediately produce a circular path – it only tests whether one exists. But to find one, simply choose any vertex that remains and follow its edges until it returns to some vertex already traversed. That will always happen since there are only finitely many vertices, and none of them have out-degree = 0. Note that the vertex you choose may not be part of the circular path that you found this way. In fact, it won’t be part of any circular path if its in-degree = 0.
The script for the circularity test is the following:
/*
Script: Circularity test for email lists
Platform: SQL Server 2005
Purpose: This script accepts a table of email
re-directions and determines if
circularity exists.
Redirections are represented by a table called Edge
whose columns LHS and RHS represent the left and
right-hand sides of a re-direction.
Output: List of re-directions containing all circular paths
Comment: This test will destroy Edge, so a working copy is used
*/
-- No counting
SET NOCOUNT OFF
-- Make working copy of Edge
IF EXISTS (SELECT* FROM sys.objects WHERE object_id =OBJECT_ID(N'[dbo].[EdgeTemp]') ANDtype in (N'U'))
DROP TABLE [dbo].[EdgeTemp]
SELECT LHS, RHS INTO EdgeTemp FROM Edge
CREATE INDEX NDX_EdgeTemp_RHS ON EdgeTemp(RHS)
-- Recursively delete edges whose RHS vertices have out-degree = 0.
-- Note that the RHS of such edges will disappear from Edge.
-- So will the LHS of such edges if they have out-degree = 1.
-- Note that @@ROWCOUNT = 0 at this point.
DELETE
FROM EdgeTemp
WHERE RHS NOT IN (SELECTDISTINCT LHS FROM EdgeTemp)
-- If @@ROWCOUNT > 0 at this point, then continue
WHILE @@ROWCOUNT > 0
DELETE
FROM EdgeTemp
WHERE RHS NOTIN (SELECTDISTINCT LHS FROM EdgeTemp)
-- Original graph will have no circular paths
-- if and only if there are no remaining edges
-- in its working copy.
-- All edges will have out-degree > 0 at this point.
SELECT * FROM EdgeTemp
-- Drop working table
DROP TABLE EdgeTemp
This test concludes with a list of edges containing all circular paths.
Showing that at most one path exists between any two vertices can be tested in the following way: Copy each edge to a temporary collection. Initially, this collection can be viewed as the LHS and RHS of all paths of length 1. Then match the RHS of each edge of the graph with the LHS of any member in the collection, adding the LHS of the edge and the RHS of the member to the collection. Now we have the LHS and RHS of all paths of length 1 or 2. Repeat this matching (using just the newly-introduced members of length 2) to get the LHS and RHS of all paths of length 1, 2, or 3. Continue this way until no more new edges are available for the next iteration of this recursion. After that, no duplicate records exist in the temporary collection if, and only if, there is at most one path between any two vertices of the original graph.
Now if you’re still awake, notice that the second test assumes that there are no circular paths! Otherwise, you’ll go into an infinite loop. So the first test must succeed before the second test is even performed.
So let’s change the above example by truncating the edge 9 -> 10. Now there are no circular paths and we can perform the second test:
The first iteration produces the LHS and RHS of all paths of length 1 (i.e. all edges):
| LHS | RHS | LHS | RHS | LHS | RHS | LHS | RHS | LHS | RHS | LHS | RHS | LHS | RHS | ||||||
| 1 | 12 | 2 | 12 | 3 | 14 | 4 | 5 | 5 | 13 | 6 | 9 | 7 | 6 | ||||||
| 8 | 15 | 9 | 8 | 10 | 7 | 10 | 11 | 10 | 13 | 10 | 16 | 11 | 16 |
The next iteration produces the LHS and RHS all paths of length 2:
| LHS | RHS | LHS | RHS | LHS | RHS | LHS | RHS | LHS | RHS | LHS | RHS | |||||
| 4 | 13 | 6 | 8 | 7 | 9 | 9 | 15 | 10 | 6 | 10 | 16 |
The next iteration produces the LHS and RHS all paths of length 3:
| LHS | RHS | LHS | RHS | LHS | RHS | ||
| 6 | 15 | 7 | 8 | 10 | 9 |
The next iteration produces the LHS and RHS all paths of length 4:
| LHS | RHS | LHS | RHS | |
| 7 | 15 | 10 | 8 |
The final iteration produces the LHS and RHS all paths of length 5:
| LHS | RHS |
| 10 | 15 |
Note that duplicate LHS, RHS combinations produced in a given iteration must represent different paths (use simple induction on the preceding iteration to prove this). But paths represented by those LHS, RHS combinations in different iterations have different lengths (by construction) so they must be different paths. Therefore, duplicate LHS, RHS combinations always represent different paths between the same pair of vertices. So in our truncated example, there are two paths from 10 to 16 and no other redundancy exists.
We will use SQL Server 2005’s elegant Common Table Expressions to seek duplicates while recursively listing the LHS, RHS combinations. This test will output all pairs of vertices with multiple paths between them, and count how many there are. Optionally, you may use the diagnostics option to list the iterations.
The script for the redundancy test is the following:
/*
Script: Redundancy test for email lists
Platform: SQL Server 2005
Purpose: This script accepts a table of email
re-directions and determines if
any recipient received multiple emails.
Redirections are represented by a table called Edge
whose columns LHS and RHS represent the left and
right-hand sides of a re-direction.
Output: Number of redundant paths between any pair of emails having them
Note: Assumes no circular paths with re-directions.
Otherwise, script will go into an infinite loop.
Use sister script to check this beforehand.
*/
-- No counting
SET NOCOUNT ON
-- Determine redundant paths between any pair of emails, and count them
;WITH Collect AS
(
-- Collect the LHS and RHS of all paths of length L = 1 (i.e. all edges).
-- Use i to record iteration for diagnostics.
SELECT i= 1, LHS, RHS
FROM Edge
UNION ALL -- Must use ALL because duplicates will always represent different paths
-- Collect the LHS and RHS all paths of length L
-- by joining re-directions with previously collected paths
-- in the collection of length L - 1
SELECT i = i + 1, Edge.LHS, Collect.RHS
FROM Edge INNER JOIN Collect
ON Edge.RHS = Collect.LHS
)
-- Output result.
-- Set MAXRECURSION to 0 to allow unlimited recursion.
SELECT LHS, RHS,COUNT(*) AS NumPath FROM Collect GROUP BY LHS,RHS HAVING COUNT(*)> 1 OPTION (MAXRECURSION 100)
-- Diagnostics:
-- SELECT i, LHS, RHS FROM Collect ORDER BY CAST(i AS INT), CAST(LHS AS INT), CAST(RHS AS INT) OPTION (MAXRECURSION 100)
Finally, here’s a simple script to produce random graphs for testing:
/*
Script: Produce random directed graph
Platform: SQL Server 2005
Purpose: This script builds a random directed graph called Edge
*/-- No counting
SET NOCOUNT ON
-- Declarations
DECLARE @Vertex1 INT
DECLARE @Vertex2 INT
-- Create Edge
IF EXISTS (SELECT * FROM sys.objects WHERE object_id =OBJECT_ID(N'Edge')AND type in(N'U'))
DROP TABLE Edge
CREATE TABLE Edge(
LHS varchar(255),
RHS varchar(255)
)ON [PRIMARY]
-- Initialise the first vertex
SET @Vertex1 = 0
-- Enumerate all pairs of vertices from 1 to 10,
-- where the second vertex is less than the first,
-- and create a directed edge with 20% probability
-- on each pair chosen (50% either way for those chosen).
-- Note that higher probabilities will create more edges.
WHILE @Vertex1 < 10 -- Number of vertices to build
BEGIN
SET @Vertex1 = @Vertex1 + 1
SET @Vertex2 = 1
WHILE @Vertex2 < @Vertex1
BEGIN
-- 20% probability of creating directed edge (i.e. 1 out of 5)
IF CONVERT(INT, 5*RAND())= 1
-- 50% probability direction goes this way (i.e. 1 out of 2)
IF CONVERT(INT, 2*RAND())= 1
INSERT INTO Edge(LHS,RHS)VALUES(@Vertex1, @Vertex2)
ELSE
-- 50% probability direction goes that way
INSERT INTO Edge(LHS,RHS)VALUES(@Vertex2, @Vertex1)
SET @Vertex2 = @Vertex2 + 1
END
END
-- Index Edge
CREATE INDEX IDX_Edge_RHS ON Edge(RHS)
-- Display graph
SELECT * FROM Edge
After producing a random graph, run the first test for circularity. If it’s successful (and only if it’s successful), run the second test for redundancy. Otherwise, produce another random graph and start over.
Randomly generated graphs readily produce circular paths, unlike those built manually from real broadcasts, where most emails are directed to external sites (where we know nothing about their re-directions). You can adjust the probabilities to influence how many circular paths should be created. Of course, performance will be an issue with the second test on large non-sparse graphs since the expected number of paths goes up very quickly with the number of edges. Fortunately, real broadcasts are relatively sparse and well-behaved. In practice, however, even one redundancy is one too many since its affect on customers can be quite annoying.
An enhanced version of these scripts is used by a mid-size marketing company to verify the integrity of their broadcasts, which change monthly. Users submit their re-directions to their email coordinator, who verifies the collated lists before sending them to their email administrator. And that saves everybody phone calls and manual debugging.
The above scripts are quite general, and may be applied to any situation where hierarchies exist in the form of directed graphs.




