Sung woefully to the tune of 'Yesterday' by the Beatles:

Hierarchiessssssss…

Running slower than they need to beeeee!

I've got angry users calling meeeee!

Ohhhhhh, hier-ar-chies run so slowwww-ly!

Oh, oh, oh, oh, oh, oh, oh.

Introduction

If you've had to work with hierarchical data to any great extent in SQL Server, then you know that there are many different types of hierarchical structures and that each has its own set of advantages and disadvantages. Unfortunately, the advantages of each structure typically don't overlap with the advantages of the other structures.

Two of my favorite hierarchical structures are the Adjacency List and the Nested Sets structures.

I really like Adjacency Lists because they're easy for humans to understand and very easy to make changes to. If something goes wrong with an Adjacency List, even a human can usually fix them with relative ease because each and every node is "aware" of only one other node. Unfortunately, they're difficult to use because they require relatively slow and complicated procedural or recursive code just to traverse the hierarchy never mind doing something more complicated such as aggregating the data and sorting the output for human consumption. The bottom line for Adjacency Lists is that they're simple to maintain but slow and complicated to use.

I also really like Nested Sets because they're easy to use and lightning-quick at all the things that Adjacency Lists are so slow and cumbersome at doing. The problem with Nested Sets is that they're very difficult for humans to put together and maintain. Even with the help of a computer, a new node inserted near the beginning of the hierarchy requires recalculation of most of the anchor points that make up the Nested Sets. Further, if something goes haywire with the anchor points, it's nearly impossible for most humans to repair them in a timely manner because a single node is related to many nodes instead of just one. I don't use the relatively new HierarchyID data-type for many of the same reasons mentioned above.

To get the advantages of both the Adjacency List and Nested Sets with few of the disadvantages of either isn't as difficult as many would think. "All" you have to do is rebuild the Nested Sets from the Adjacency List every time you make a change to the Adjacency List. Since most hierarchies are relatively small and don't change very often, an overnight run to do such a rebuild with conventional push-stack methods is acceptable to most.

BUT, what if you have hierarchies with a million or more nodes in them? What if you need to make frequent changes to such a large hierarchy? What if you have a new million node Adjacency List from a third party that, according the boss breathing down your neck, needs to be converted RIGHT NOW? A build or rebuild of the Nested Sets from a large Adjacency list may not actually finish overnight using traditional methods for such large hierarchies. So, what do you do? What CAN you do?

The answer is… do a little math… and get a Tally Table involved.

The purpose of this article is to show you how to convert a 'well formed' Adjacency List to Nested Sets faster than you could have ever imagined.

Who This Article Is For

Most of the articles I've written in the past have included just about everything you need to know to make it through the article. In the case of hierarchies, whole books, hundreds of chapters, and thousands of Internet articles have been written on the subject and it's impossible for me to cover all of the aspects of the subject in a single article. For that reason, I have to make certain assumptions in this article. For example, I have to assume that you already know what the Adjacency List and Nested Sets structures are and how they are used. I have to assume that you know how to prevent "cycles" in an Adjacency List. I have to assume that you already know what a Tally Table is and how it can be used to replace certain types of loops. And, I have to assume certain basic knowledge on your part of some common T-SQL functionality such as knowing what  "'CTE"s and "Recursive CTE"s are and how they work.

I can help you get started on what a Tally Table is and how it can be used to replace certain loops by referring you to the following article right here on SQLServerCentral.

http://www.sqlservercentral.com/articles/T-SQL/62867/

Last but not least, I wrote this article and code so that anyone still having to use SQL Server 2005 (and up) could enjoy the benefits of high performance hierarchies. That's also why I don't touch on the "new" HierarchyID so much in this article. It's simply not available in SQL Server 2005.

Some Jargon

I also assume that you already know most hierarchical terminology such as what a "node" and an "edge" are but there are certain terms that I've borrowed from the MLM (Multi-Level Marketing) industry to keep my explanations shorter and, hopefully, easier to understand.

Downline

Since most org charts and similar trees are physically displayed with the Root Node at the top and the Leaf Nodes at the bottom, certain types of businesses known as "MLMs" (Multi-Level Marketing) use the term "Downline" to simplify saying "all of the descendants for the given node". In other words, it contains all of the child nodes from the given node down to the Leaf Nodes. It comes from the fact that all the descendants are physically located 'own' from the given node on an org chart.

Upline

The opposite of the "Downline". Basically, it means "all of the ancestors for a given node". If you were to color in all of the nodes in the upline for a given node, there would only be one colored node from the given node to the Root Node at each level of the hierarchy. As you'll find out in this article, that's an incredibly important concept in some of the simple formulas we're going to use.

Sort Path

You probably know this as the "Materialized Hierarchical Path" or similar terminology. It contains a concatenated (and usually delimited) list of the entire upline for a given node with the Root Node being farthest to the left and the given node being farthest to the right. What many people don't know is that it can also be used for sorting purposes so I simplified the term as "Sort Path".

Test Data

The very premise of this article is based on a huge claim of a very high performance replacement for a process that usually takes much longer than most of us can tolerate in our code. Of course, such a claim must be backed up by demonstrable proof in the form of code. The problem with that is (please pardon the pun) that the data for large hierarchies doesn't grow on trees. Very few sets of large hierarchical data are available on the Internet and, although there's some code to build one, they usually take longer than we're willing to wait to build even a relatively small test hierarchy.

We also need a smaller, easy to understand hierarchy that we can all relate to as an easy-to-display and understand diagram.

Last but not least, we need to be able to easily switch back and forth between the larger and smaller hierarchies with ease and without having to change any of our code.

For those reasons, I've created two stored procedures, one to quickly and easily create a programmable-sized large hierarchy and another to create a fixed size hierarchy to be used for explaining various methods. Since the code drops and recreates tables, all of the test code is setup to execute in TempDB so we don't accidentally overwrite a real table that you may be using.

Those two stored procedures are located in the "HierarchyCode.zip" file in the "Resources" section near the end of this article. If you intend to follow along in this article, I recommend that you unzip that file and execute both of the scripts now (BuildSmallEmployeeTable.sql and BuildLargeEmployeeTable.sql) to create the two stored procedures.

Both procedures build tables with identical structures. They contain an EmployeeID, ManagerID, and EmployeeName. Both have been indexed for the best performance possible by all other code in this article that uses them (you can use these indexes to cross-check your own tables). Both tables are named "dbo.Employee" and cannot exist at the same time.

As a bit of a side bar, I use TempDB for almost all of my experiments even if I'm on a Dev box. I just don't want to take the chance of dropping someone's very commonly named Employee table by mistake.

The 'BuildLargeEmployeeTable' Stored Procedure

With the understanding that how this stored procedure works is well beyond the scope of this article (although the code is heavily documented if you're interested), the "dbo.BuildLargeEmployeeTable" stored procedure will build a "well formed" Adjacency List in a table called "dbo.Employee" in TempDB. The first (required) parameter is used to identify the number of nodes the hierarchy should contain and will build a million node hierarchy on my 4 processor (i5), 6GB laptop in about 7 seconds. You can add a non-zero value for a second (optional) parameter to randomize the IDs in a fashion that more closely resembles a large hierarchy in real life. Of course, that takes a bit of extra time but I believe you'll still be happy with how fast it does its job especially when you realize that it built a million rows in just 17 seconds.

Please see the comments in the stored procedure if you'd like more details. Here's an example call of this stored procedure to create a million node Employee table.

   EXEC dbo.BuildLargeEmployeeTable 1000000,1;

The "BuildSmallEmployeeTable" Stored Procedure

The "dbo.BuildSmallEmployeeTable" stored procedure is fairly straight forward. It conditionally drops the "dbo.Employee" table and rebuilds it with fixed data that we'll use throughout this article to explain what's happening with the new conversion process.

Here's the call to the stored procedure to build the small Employee table. It takes no parameters.

   EXEC dbo.BuildSmallEmployeeTable;

Here's a picture of the data partially created by the "dbo.BuildSmallHierarchy" stored procedure above. As you can see, it's a small organizational chart.

Each node has 4 lines of data in it (a total of 5 columns of information). The first 3 items below are included in the build by the "dbo.BuildSmallEmployeeTable" stored procedure.

1. The first line contains the name of the employee and is contained in the Employee table. The name of the individual is included just for easier reference when talking about the nodes and will not show up in the final table we're going to build.
2. The second line contains the EmployeeID and is contained in the Employee table.
3. The third line contains the ManagerID of the employee and is contained in the Employee Table.
4. The fourth line contains two pieces of information that aren't contained in the Adjacency List. The two numbers on that line are the "left" and "right" values for the Nested Sets that we've yet to build.

What are "Bowers"?

In most discussions concerning Nested Sets, the two numbers for the "left" and "right" values of the Nested Sets live in rather nondescript columns called "'lft" and "rgt". BWAA-HAAA!!! I can just see Abbott and Costello now.

Costello: Which column is the right column to sort by? This one (pointing to the "rgt" column)?

Abbott: No, you need to sort by the left column.

Costello: Are you sure that's the right column?

Abbott: No, I just told you it's the left column and that's the right column to sort by.

To avoid that kind of confusion, I call the columns the "LeftBower" and the "RightBower". Why "Bower"? The two large anchors on the front of large ships are called "Bowers". Since the two numbers serve as "anchors" for each node in Nested Sets and since I'm ex-Navy, it just seemed logical to me.

The Push Stack Method

Before we start on the new process for converting an Adjacency List to Nested Sets, let me show you the traditional method also known as the "Push-Stack" method. It's very procedural (RBAR¹ on steroids). Here's what it looks like when plotted against the org chart.

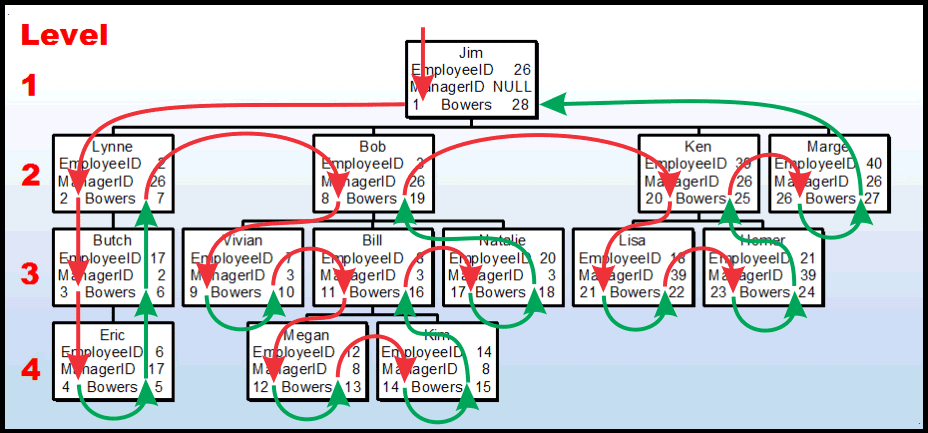
If you look at the Left and Right Bowers starting at "1" in the node for "Jim", each Red arrow represents a "Push" of data onto a "stack". Each Green arrow represents a "Pop" from the stack. "Pushes" create the LeftBower and "Pops" create the RightBower.

What the diagram doesn't show is that each push does a joined SELECT between a sacrificial copy of the original table and the final table that contains the Nested Sets. Each push also contains a joined INSERT between the two tables followed by a DELETE from the sacrificial table. Each pop does the same initial joined SELECT that a push does and then does an UPDATE on the final table.

What that means is that, except for the Root Node, every node suffers two joined SELECTs, a joined INSERT, a DELETE, and an UPDATE in order to build the Nested Sets. What that also means for a million node hierarchy is that there are at least 5 million execution plans that need to be evaluated (even if reused) and executed.

All of that also means slow and resource intensive. You can also add the word "deceitful" because you might be tricked into thinking that it's not so bad if you run the push-stack method on a small hierarchy of just 10,000 nodes. When you run it on larger hierarchies, you'll soon find out that the code gets much worse very quickly as the number of nodes grows.

I tweaked some push-stack code that I found on the Internet by changing the table names, column names, and related data types to match the Employee tables that our test data generation procs make. It was really slow so I tweaked it again to make it run 3 times faster by converting some of it to SQL Server proprietary code and adding some indexes to the tables it creates. By all other standards, it's still slow.

Here are the results from 4 different runs of the push-stack conversion code. You can see the first indication of a major performance problem between just 1,000 and 10,000 nodes because 10 times the number of nodes took 70 times longer instead of just 10 times longer.

Duration for 1,000 Nodes = 00:00:00:870

Duration for 10,000 Nodes = 00:01:01:783 (70 times slower instead of just 10)

Duration for 100,000 Nodes = 00:49:59:730 (3,446 times slower instead of just 100)

Duration for 1,000,000 Nodes = 'Didn't even try this'

In case you'd like to try the same experiments on your own, the push-stack code I ended up with is also in the "HierarchyCode.zip" file in the "Resources" section near the end of the article.

Now you know why people have developed so many different ways of trying to maintain Nested Sets once they're built. It just takes too long to use traditional methods to convert from the simple-to-maintain Adjacency List to the high performance Nested Sets structure.

That's about to change, though.

Set Based Code to Calculate the Bowers

Ok… we've seen that the typical RBAR¹ push-stack methods for converting an Adjacency List to Nested Sets just aren't going to be able to do what we want in a hurry especially if we have a large hierarchy of a million nodes or more. If we extrapolate the time it would take to convert a million nodes, we end up with a run time of about 2 days, certainly not an overnight run by any means.

So, let's build a better way using a little math and a Tally Table. We'll also see some of the problems that may have, up ‘till now, prevented most folks from combining large Adjacency Lists with Nested Sets.

Calculating the Left Bower

The math for calculating the Left Bower is incredibly simple. Let's use the same small hierarchy org chart you saw before to see how it works.

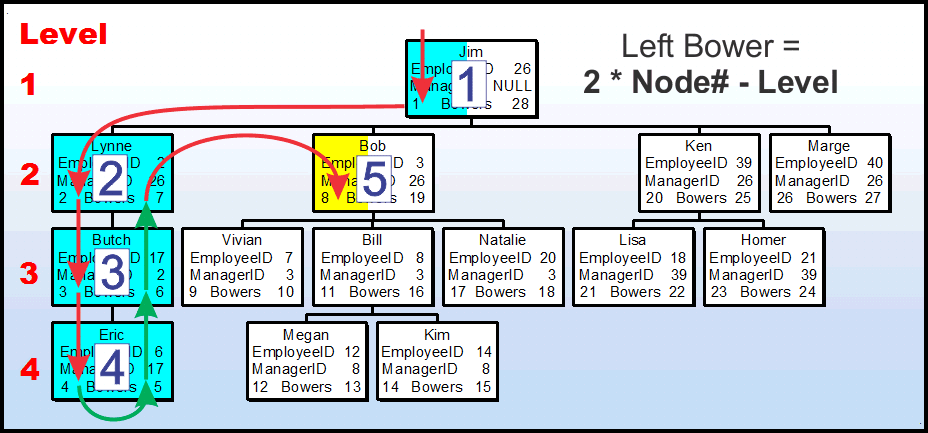
For this example, we're trying to calculate the Left Bower for "Bob". You'll grow to appreciate Bob because we're going to work him to death in these examples.

Notice the colored nodes. If we were to use the push stack method, they represent the nodes that we've passed through (or "touched") to get to the Left Bower of Bob. If a node is fully colored, then we've passed through the node twice ("touched" both nodes) and we "know" both Bowers for those nodes. If we've only passed through ("touched") the node once, then only the side with the "known" Bower has been colored. We're on the 5th node (Bob's node) but haven't yet calculated the Left Bower which is why it's colored differently than the other nodes even though we're currently "touching" the Left Bower.

So, first of all, Bob is the 5th node in the "chain" that would have been formed by the push-stack method. For purposes of this article, we call that number the "Node Number".  Each node has 2 Bowers and if we multiply the number of Bowers per-node by Bob's node number, we get the number "10". We're not done yet, though.

Out of those 5 nodes, how many Bowers would the push-stack process have NOT yet "touched"? Those are indicated by the uncolored side of the partially colored nodes. In this case, the answer is once again "2". Here's where that important concept about the upline that I mentioned in the "Jargon" section of this article comes into play. It turns out that the "Level" of the given node ("2" for Bob's node) will ALWAYS correctly indicate the number of Bowers not yet "touched" if we were using the push-stack method. Don't forget that the upline will ALWAYS consist of just one node per level.

Plugging all the numbers into the formula that I've displayed in the upper right corner of the graphic above, we end up with (2*5)-2 or '8' Bob's Left Bower is '8'

Let's try the same thing with Kim.

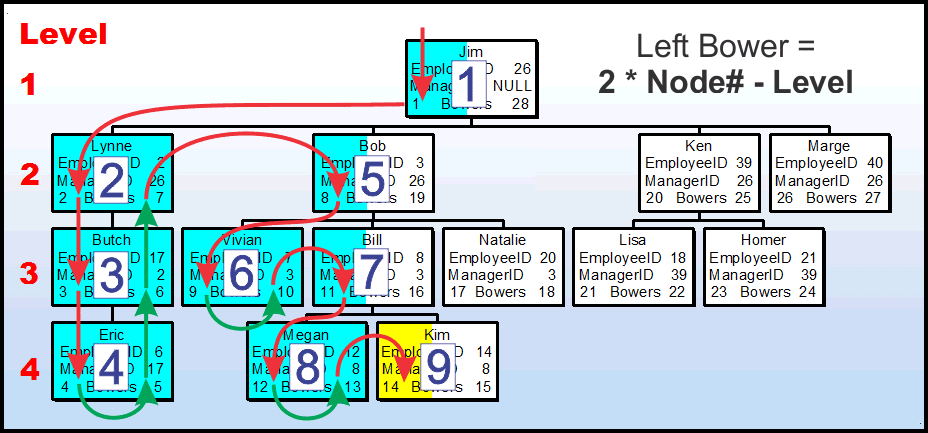
Using the same concept as we did with Bob, we've numbered the nodes in the order that they're first encountered by the push-stack method and have colored the nodes as to whether both Bowers have been "touched" (fully colored box) or just one Bower has been "touched" (half colored box). Notice that we've only "touched" the Left Bower of every node in Kim's upline and that number of nodes is the same as the Level that Kim's node is at, which is "4".  Kim's node number is "9" because it's the 9th node that would have been "touched" by the push-stack method.

Using the same formula as before, we end up with (2*9)-4 which is 18-4 or 14 and we can see that we've correctly calculated Kim's left node.

Now, isn't that easy? Yeah… I know… wait for it. 😉

The most obvious problem is that we need to know the node numbers and they need to be in the same order as if we used the push-stack method. On top of that, we also need to know the Level number. How in the world are we going to do all of that? We need a miracle to solve the equation of '2 * (insert miracle here) – (insert another miracle here)'. Actually, we need 4 miracles. 1) Find and count the nodes in 2) the correct order and 3) calculate the Level and 4) do it all hundreds and even thousands of times faster than the push-stack method.

The Miracle of the 'Sort-Path'

Again, one of the proper names for the "Sort Path" is "Materialized Hierarchical Path". For each node, it contains the entire list of nodes in the upline of the given node with the Root Node furthest on the left and the given node furthest on the right. Since we could have a whole lot of nodes in each "Sort Path" on a really deep hierarchy, each node needs to be stored in as compact a format as possible but also needs to be in the same format for every node to be sortable for our purposes. This is kind of the way that a HierarchyID works except the HierarchyID works using positional notation rather than by factual notation (EmployeeID) like we're going to.

Each EmployeeID is stored as an integer in the Adjacency List (Employee table). An integer is 4 bytes whether it contains the value zero or two billion (for example). The value of each integer can easily be stored as 4 bytes in the BINARY and VARBINARY data-types.

To summarize what we're about to do…

1. Read ALL the nodes in a given level as indicated by the parent/child relationship in the Adjacency List.
2. As we read the nodes in a given level, mark each node with the current level number.
3. As we read the nodes in a given level, convert the EmployeeID to a Binary(4) and concatenate it with the parents in the previous level's binary string of EmployeeID's. This will build the Sort Path.
4. Number the rows according to the Sort Path. This will number the rows in the same order that the push-stack method would number them.
5. Once the data from Steps 1, 2, 3, AND 4 are complete, update that data with the calculated Left Bower.

Sounds like a whole lot of complicated work, doesn't it? It's not though. A single recursive CTE could easily do all 5 steps but I happen to know that things will run much faster later if we use some 'Divide'n'Conquer' methods and only use the recursive CTE to do the first 4 steps. In the process, we'll build the final table directly.

Here's the code for all 5 Steps.

--===========================================================================
--      1.  Read ALL the nodes in a given level as indicated by the parent/
--          child relationship in the Adjacency List.
--      2.  As we read the nodes in a given level, mark each node with the 
--          current level number.
--      3.  As we read the nodes in a given level, convert the EmployeeID to
--          a Binary(4) and concatenate it with the parents in the previous
--          level's binary string of EmployeeID's.  This will build the 
--          SortPath.
--      4.  Number the rows according to the Sort Path.  This will number the
--          rows in the same order that the push-stack method would number 
--          them.
--===========================================================================
--===== Since we're going to drop and create tables, do this in a nice, safe 
     -- place that everyone has.
    USE TempDB;
--===== Conditionally drop Temp tables to make reruns easy
     IF OBJECT_ID('dbo.Hierarchy','U') IS NOT NULL
        DROP TABLE dbo.Hierarchy;
--===== Build the new table on-the-fly including some place holders
   WITH cteBuildPath AS 
( --=== This is the "anchor" part of the recursive CTE.
     -- The only thing it does is load the Root Node.
 SELECT anchor.EmployeeID, 
        anchor.ManagerID, 
        HLevel   = 1,
        SortPath =  CAST(
                        CAST(anchor.EmployeeID AS BINARY(4)) 
                    AS VARBINARY(4000)) --Up to 1000 levels deep.
   FROM dbo.Employee AS anchor
  WHERE ManagerID IS NULL --Only the Root Node has a NULL ManagerID
  UNION ALL 
 --==== This is the "recursive" part of the CTE that adds 1 for each level
     -- and concatenates each level of EmployeeID's to the SortPath column.  
 SELECT recur.EmployeeID, 
        recur.ManagerID, 
        HLevel   =  cte.HLevel + 1,
        SortPath =  CAST( --This does the concatenation to build SortPath
                        cte.SortPath + CAST(Recur.EmployeeID AS BINARY(4))
                    AS VARBINARY(4000))
   FROM dbo.Employee      AS recur
  INNER JOIN cteBuildPath AS cte 
          ON cte.EmployeeID = recur.ManagerID
) --=== This final SELECT/INTO creates the Node # in the same order as a
     -- push-stack would. It also creates the final table with some
     -- "reserved" columns on the fly. We'll leave the SortPath column in
     -- place because we're still going to need it later.
     -- The ISNULLs make NOT NULL columns.
 SELECT EmployeeID = ISNULL(sorted.EmployeeID,0),
        sorted.ManagerID,
        HLevel     = ISNULL(sorted.HLevel,0),
        LeftBower  = ISNULL(CAST(0 AS INT),0), --Place holder
        RightBower = ISNULL(CAST(0 AS INT),0), --Place holder
        NodeNumber = ROW_NUMBER() OVER (ORDER BY sorted.SortPath),
        NodeCount  = ISNULL(CAST(0 AS INT),0), --Place holder
        SortPath   = ISNULL(sorted.SortPath,sorted.SortPath)
   INTO dbo.Hierarchy
   FROM cteBuildPath AS sorted
 OPTION (MAXRECURSION 100) --Change this IF necessary
;
--===========================================================================
--      5.  Once the data from Steps 1, 2, 3, AND 4 is complete, update that
--          data with the calculated Left Bower.
--===========================================================================
--===== Calculate the Left Bower
 UPDATE dbo.Hierarchy
    SET LeftBower = 2 * NodeNumber - HLevel
;
--SELECT * FROM dbo.Hierarchy

If you first run EXEC dbo.BuildSmallEmployeeTable to create the small Employee table and then run the script above, here's what you'll get in the new dbo.Hierarchy table that it creates.

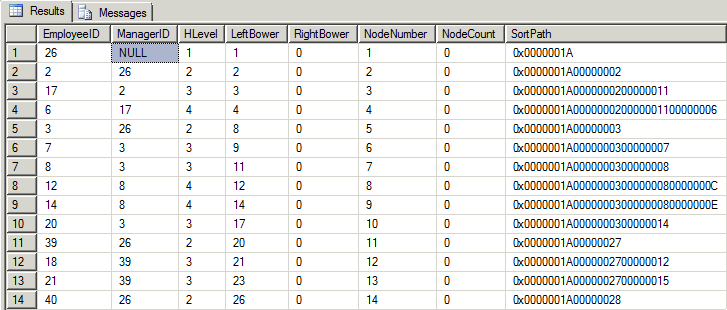
VARBINARY data is displayed as hexadecimal in SSMS query results. If you look at the SortPath column, which contains the concatenated hex equivalents of each EmployeeID in the upline of each node, you can easily see how it can be used to sort. Also notice that every level of the given node's upline is included in the sort path. Just group the SortPath column by every 8 characters (2 characters per byte starting after the '0x') and you can see the individual hex equivalents for each EmployeeID. THAT will be very important in the next steps.

Also, we didn't need to save the NodeNumber column in the table but I left it there just so that we can easily verify that the LeftBower calculation that used it has actually worked correctly on this small but detailed hierarchy.

By the way, the code above completes on a 100,000 node hierarchy on my laptop in just over 3 seconds! That's only about 998 times faster than the push-stack method, so far. It'll be thousands of times faster for a million nodes even after we calculate the Right Bower. If you want to try what we have so far, execute EXEC dbo.BuildLargeEmployeeTable 100000 to build a 100,000 node Employee table and then run the code above.

Four miracles down. Three to go.

Calculating the Right Bower

Just like there is an "easy" formula to calculate the Left Bower, so it is with the Right Bower. Let's see how that's calculated for "Bob".

Once again, the fully colored Blue nodes represent nodes that we've "touched" twice if we used the push-stack method, which is represented by the Red and Green arrows. We've also "touched" (and successfully calculated) Bob's Left Bower and know that it has a value of "8" because we just got done calculating it.

If we find ALL of the nodes in Bob's downline including Bob, we end up with 6 nodes, 5 of which have 2 Bowers calculated (the Blue nodes) and one (Bob's node) of which has only 1 Bower calculated. So, just like the formula says in the upper right corner of the graphic above, if we count all of the nodes, subtract 1 (Bob's node) so we're only working with the Blue nodes (Bob's downline), multiply by the number of Bowers each node has (2), add that to Bob's Left Bower, and add the number of Bowers already calculated for Bob (1), we end up with the correct value for the Right Bower. In other words (6 Nodes -1) * 2 + 8 + 1 = (5 * 2) + 9 = 10 + 9 = 19.

Try the same thing with any of the other nodes (even Jim's node) and see that it works for every node.

As a side bar, the formula could be simplified a bit by counting only the Blue nodes to begin with. Don't do that, though. The formula is meant to simplify the counting step that's coming up.

So what's the rub here? The answer is that we haven't yet calculated how many nodes are in Bob's downline and we haven't actually calculated the Left or Right Bowers for any of the nodes in Bob's downline. It's almost like we need to know the Nested Sets before we can calculate the Nested Sets.

We need three more miracles. We need to 1) find all the nodes in Bob's downline and 2) count them and 3) still do it as fast as possible.

The 'Tally Table' Miracle

If we execute the code to generate the small hierarchy table (EXEC dbo.BuildSmallEmployeeTable) and run the Left Bower code we previously created, we get a result set that looks like the graphic below. While you're looking at it, remember that I said that the SortPath contains ALL of the nodes in each given node's upline. Bob's downline nodes are no exception.

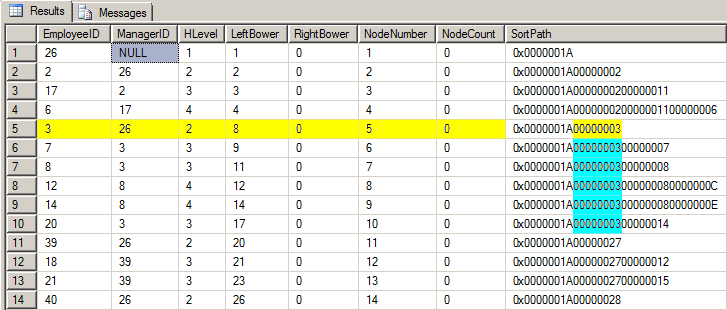
Bob's node information is highlighted in yellow in the graphic above. Bob appears in the SortPath of 5 other (Blue) nodes. This is Bob's downline. All we have to do is split the SortPath by Level and count the number of occurrences of each and every EmployeeID that appears in the SortPath.

That's where the miracle of a specially formed Tally Table will come into play. Let's write the code to split the SortPath nodes and count them all at once in a Set Based fashion.

First, what do we need to store in the special Tally Table (which we'll call 'HTally' from here on out)? We need the starting position of each EmployeeID in the SortPath. If you'll recall, each EmployeeID was saved as a BINARY(4) meaning that each EmployeeID takes up 4 bytes in the SortPath column. The first EmployeeID starts at position 1 and continues for 4 bytes. The second EmployeeID starts 4 characters after the first starting position of 1, which means it starts at 5, and continues for 4 bytes. Likewise, the third EmployeeID starts at 9 and continues for 4 bytes and so on. Also remember that each set of 4 bytes vertically covers a level (HLevel).

In other words, our HTtally Table needs to have the numbers 1, 5, 9, etc in it for as many levels as there are in the entire hierarchy. I'm going to use a real table for this just to keep the code simple. You certainly could build one on-the-fly using Itzik Ben-Gan's famous "cascading CTE" ("cCTE" for short) trick.

Here's one way to build the HTally Table, which will handle up to 1,000 levels, in this case. It only needs to be built once since it becomes a permanent table. For this demonstration, please run the following code in TempDB because that's where everything else we've done, so far, lives.

--===== Create the HTally table to be used for splitting SortPath
 SELECT TOP 1000 --(4 * 1000 = VARBINARY(4000) in length)
        N = ISNULL(CAST(
                (ROW_NUMBER() OVER (ORDER BY (SELECT NULL))-1)*4+1
            AS INT),0)
   INTO dbo.HTally
   FROM master.sys.all_columns ac1
  CROSS JOIN master.sys.all_columns ac2
;
--===== Add the quintessential PK for performance.
  ALTER TABLE dbo.HTally
    ADD CONSTRAINT PK_HTally 
        PRIMARY KEY CLUSTERED (N) WITH FILLFACTOR = 100
;

Next, we'll not only do the split and remember the NodeCount, but we'll also calculate the Right Bower. Don't blink. This is incredibly fast for what it's actually doing.

WITH cteCountDownlines AS
( --=== Count each occurrence of EmployeeID in the sort path
 SELECT EmployeeID = CAST(SUBSTRING(h.SortPath,t.N,4) AS INT), 
        NodeCount  = COUNT(*) --Includes current node
   FROM dbo.Hierarchy h, 
        dbo.HTally t
  WHERE t.N BETWEEN 1 AND DATALENGTH(SortPath)
  GROUP BY SUBSTRING(h.SortPath,t.N,4)
) --=== Update the NodeCount and calculate the RightBower
 UPDATE h
    SET h.NodeCount  = downline.NodeCount,
        h.RightBower = (downline.NodeCount - 1) * 2 + LeftBower + 1
   FROM dbo.Hierarchy h
   JOIN cteCountDownlines downline
     ON h.EmployeeID = downline.EmployeeID
;

Here's what you get as a result from the small hierarchy example.

SELECT * FROM dbo.Hierarchy ORDER BY LeftBower; --Wow! Another way to sort!

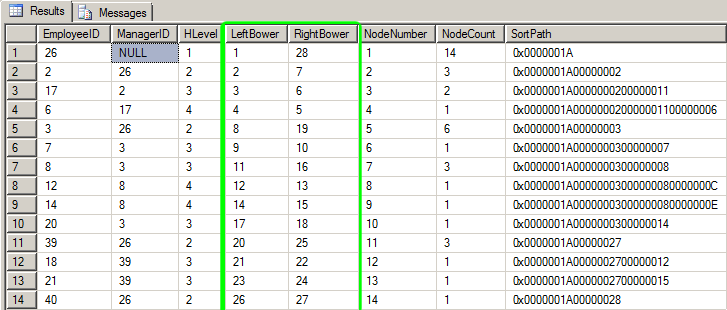
What we have here is the best of several worlds. The EmployeeID and ManagerID make up the Adjacency List. The SortPath makes up a "Materialized Hierarchy Path" which contains some useful information should we ever need it. The LeftBower and RightBower columns make up the Nested Sets. And, not that we need them but we have some nice 'warm fuzzy' columns like HLevel, NodeNumber, and NodeCount (MLMers will need this column as well as HLevel to calculate payouts). HLevel could actually be used to control indentation at the GUI or Report level.

All we need to do now is add some indexes and "Bob's your Uncle".

The Final Code

Let's put all of this together in a nice, easy to use, stored procedure. In the process, we'll knock out one additional table scan by combining the creation of the Left and Right Bowers into a single piece of code using SQL Server's proprietary and highly useful version of UPDATE.

I've included lots of documentation in the code.

 CREATE PROCEDURE dbo.RebuildNestedSets AS
/****************************************************************************
 Purpose:
 Rebuilds a "Hierarchy" table that contains the original Adjacency List,
 the Nested Sets version of the same hierarchy, and several other useful 
 columns of data some of which need not be included in the final table.
 Usage:
 EXEC dbo.RebuildNestedSets
 Progammer's Notes:
 1. As currently written, the code reads from a table called dbo.Employee.
 2. The Employee table must contain well indexed EmployeeID (child) and
    ManagerID (parent) columns.
 3. The Employee table must be a "well formed" Adjacency List. That is, the
    EmployeeID column must be unique and there must be a foreign key on the
    ManagerID column that points to the EmployeeID column. The table must not
    contain any "cycles" (an EmployeeID in its own upline). The Root Node
    must have a NULL for ManagerID.
 4. The final table, named dbo.Hierarchy, will be created in the same 
    database as where this stored procedure is present.  IT DOES DROP THE 
    TABLE CALLED DBO.HIERARCHY SO BE CAREFUL THAT IT DOESN'T DROP A TABLE 
    NEAR AND DEAR TO YOUR HEART.
 5. This code currently has no ROLLBACK capabilities so make sure that you
    have met all of the requirements (and, perhaps, more) cited in #3 above.
 Dependencies:
 1. This stored procedure requires that the following special purpose HTally
    table be present in the same database from which it runs.
--===== Create the HTally table to be used for splitting SortPath
 SELECT TOP 1000 --(4 * 1000 = VARBINARY(4000) in length)
        N = ISNULL(CAST(
                (ROW_NUMBER() OVER (ORDER BY (SELECT NULL))-1)*4+1
            AS INT),0)
   INTO dbo.HTally
   FROM master.sys.all_columns ac1
  CROSS JOIN master.sys.all_columns ac2
;
--===== Add the quintessential PK for performance.
  ALTER TABLE dbo.HTally
    ADD CONSTRAINT PK_HTally 
        PRIMARY KEY CLUSTERED (N) WITH FILLFACTOR = 100
;
 Revision History:
 Rev 00 - Circa 2009  - Jeff Moden 
        - Initial concept and creation.
 Rev 01 - PASS 2010   - Jeff Moden 
        - Rewritten for presentation at PASS 2010.
 Rev 02 - 06 Oct 2012 - Jeff Moden
        - Code redacted to include a more efficient, higher performmance
          method of splitting the SortPath using a custom HTally Table.
****************************************************************************/--===========================================================================
--      Presets
--===========================================================================
--===== Suppress the auto-display of rowcounts to prevent from returning
     -- false errors if called from a GUI or other application.
    SET NOCOUNT ON;
--===== Start a duration timer
DECLARE @StartTime DATETIME,
        @Duration  CHAR(12);
 SELECT @StartTime = GETDATE();
--===========================================================================
--      1.  Read ALL the nodes in a given level as indicated by the parent/
--          child relationship in the Adjacency List.
--      2.  As we read the nodes in a given level, mark each node with the 
--          current level number.
--      3.  As we read the nodes in a given level, convert the EmployeeID to
--          a Binary(4) and concatenate it with the parents in the previous
--          level's binary string of EmployeeID's.  This will build the 
--          SortPath.
--      4.  Number the rows according to the Sort Path.  This will number the
--          rows in the same order that the push-stack method would number 
--          them.
--===========================================================================
--===== Conditionally drop the final table to make reruns easier in SSMS.
     IF OBJECT_ID('FK_Hierarchy_Hierarchy') IS NOT NULL
        ALTER TABLE dbo.Hierarchy
         DROP CONSTRAINT FK_Hierarchy_Hierarchy;
     IF OBJECT_ID('dbo.Hierarchy','U') IS NOT NULL
         DROP TABLE dbo.Hierarchy;
RAISERROR('Building the initial table and SortPath...',0,1) WITH NOWAIT;
--===== Build the new table on-the-fly including some place holders
   WITH cteBuildPath AS 
( --=== This is the "anchor" part of the recursive CTE.
     -- The only thing it does is load the Root Node.
 SELECT anchor.EmployeeID, 
        anchor.ManagerID, 
        HLevel   = 1,
        SortPath =  CAST(
                        CAST(anchor.EmployeeID AS BINARY(4)) 
                    AS VARBINARY(4000)) --Up to 1000 levels deep.
   FROM dbo.Employee AS anchor
  WHERE ManagerID IS NULL --Only the Root Node has a NULL ManagerID
  UNION ALL 
 --==== This is the "recursive" part of the CTE that adds 1 for each level
     -- and concatenates each level of EmployeeID's to the SortPath column.  
 SELECT recur.EmployeeID, 
        recur.ManagerID, 
        HLevel   =  cte.HLevel + 1,
        SortPath =  CAST( --This does the concatenation to build SortPath
                        cte.SortPath + CAST(Recur.EmployeeID AS BINARY(4))
                    AS VARBINARY(4000))
   FROM dbo.Employee      AS recur WITH (TABLOCK)
  INNER JOIN cteBuildPath AS cte 
          ON cte.EmployeeID = recur.ManagerID
) --=== This final INSERT/SELECT creates the Node # in the same order as a
     -- push-stack would. It also creates the final table with some
     -- "reserved" columns on the fly. We'll leave the SortPath column in
     -- place because we're still going to need it later.
     -- The ISNULLs make NOT NULL columns
 SELECT EmployeeID = ISNULL(sorted.EmployeeID,0),
        sorted.ManagerID,
        HLevel     = ISNULL(sorted.HLevel,0),
        LeftBower  = ISNULL(CAST(0 AS INT),0), --Place holder
        RightBower = ISNULL(CAST(0 AS INT),0), --Place holder
        NodeNumber = ROW_NUMBER() OVER (ORDER BY sorted.SortPath),
        NodeCount  = ISNULL(CAST(0 AS INT),0), --Place holder
        SortPath   = ISNULL(sorted.SortPath,sorted.SortPath)
   INTO dbo.Hierarchy
   FROM cteBuildPath AS sorted
 OPTION (MAXRECURSION 100) --Change this IF necessary
;
RAISERROR('There are %u rows in dbo.Hierarchy',0,1,@@ROWCOUNT) WITH NOWAIT;
--===== Display the cumulative duration
 SELECT @Duration = CONVERT(CHAR(12),GETDATE()-@StartTime,114);
RAISERROR('Cumulative Duration = %s',0,1,@Duration) WITH NOWAIT;
--===========================================================================
--      Using the information created in the table above, create the
--      NodeCount column and the LeftBower and RightBower columns to create
--      the Nested Sets hierarchical structure.
--===========================================================================
RAISERROR('Building the Nested Sets...',0,1) WITH NOWAIT;
--===== Declare a working variable to hold the result of the calculation
     -- of the LeftBower so that it may be easily used to create the
     -- RightBower in a single scan of the final table.
DECLARE @LeftBower INT
;
--===== Create the Nested Sets from the information available in the table
     -- and in the following CTE. This uses the proprietary form of UPDATE
     -- available in SQL Serrver for extra performance.
   WITH cteCountDownlines AS
( --=== Count each occurance of EmployeeID in the sort path
 SELECT EmployeeID = CAST(SUBSTRING(h.SortPath,t.N,4) AS INT), 
        NodeCount  = COUNT(*) --Includes current node
   FROM dbo.Hierarchy h, 
        dbo.HTally t
  WHERE t.N BETWEEN 1 AND DATALENGTH(SortPath)
  GROUP BY SUBSTRING(h.SortPath,t.N,4)
) --=== Update the NodeCount and calculate both Bowers
 UPDATE h
    SET @LeftBower   = LeftBower = 2 * NodeNumber - HLevel,
        h.NodeCount  = downline.NodeCount,
        h.RightBower = (downline.NodeCount - 1) * 2 + @LeftBower + 1
   FROM dbo.Hierarchy h
   JOIN cteCountDownlines downline
     ON h.EmployeeID = downline.EmployeeID
;
RAISERROR('%u rows have been updated to Nested Sets',0,1,@@ROWCOUNT)
WITH NOWAIT;
RAISERROR('If the rowcounts don''t match, there may be orphans.'
,0,1,@@ROWCOUNT)WITH NOWAIT;
--===== Display the cumulative duration
 SELECT @Duration = CONVERT(CHAR(12),GETDATE()-@StartTime,114);
RAISERROR('Cumulative Duration = %s',0,1,@Duration) WITH NOWAIT;
--===========================================================================
--      Prepare the table for high performance reads by adding indexes.
--===========================================================================
RAISERROR('Building the indexes...',0,1) WITH NOWAIT;
--===== Direct support for the Nested Sets
  ALTER TABLE dbo.Hierarchy 
    ADD CONSTRAINT PK_Hierarchy
        PRIMARY KEY CLUSTERED (LeftBower, RightBower) WITH FILLFACTOR = 100
;
 CREATE UNIQUE INDEX AK_Hierarchy 
     ON dbo.Hierarchy (EmployeeID) WITH FILLFACTOR = 100
;
  ALTER TABLE dbo.Hierarchy
    ADD CONSTRAINT FK_Hierarchy_Hierarchy FOREIGN KEY
        (ManagerID) REFERENCES dbo.Hierarchy (EmployeeID) 
     ON UPDATE NO ACTION 
     ON DELETE NO ACTION
;
--===== Display the cumulative duration
 SELECT @Duration = CONVERT(CHAR(12),GETDATE()-@StartTime,114);
RAISERROR('Cumulative Duration = %s',0,1,@Duration) WITH NOWAIT;
--===========================================================================
--      Exit
--===========================================================================
RAISERROR('===============================================',0,1) WITH NOWAIT;
RAISERROR('RUN COMPLETE',0,1) WITH NOWAIT;
RAISERROR('===============================================',0,1) WITH NOWAIT;
GO

Performance:

Here's the performance of the code above on my laptop at the same levels the push-stack method was tested at (push-stack durations included in parenthesis for comparison).

Duration for 1,000 Nodes = 00:00:00:053 (compared to 00:00:00:870)

Duration for 10,000 Nodes = 00:00:00:323 (compared to 00:01:01:783)

Duration for 100,000 Nodes = 00:00:03:867 (compared 00:49:59:730)

Duration for 1,000,000 Nodes = 00:00:54:283 (compared to something like 2 days!!!)

Note to MLM'ers

MLM hierarchies are fairly unique in the world of hierarchies. Typically, they run very deep, level wise. It may very well be that the 1000 levels (VARBINARY(4000)) and the related maximum value of the HTally Table used in this article may not be sufficient to meet your needs.

The code in this article can easily be changed to support 2,000 levels with little impact on performance.  If you need more than 2000 levels (VARBINARY(8000)), then I recommend changing to VARBINARY(MAX) and using Itzek Ben-Gan's cascading CTEs to build a cteHTally structure. Because none of the blob data-types like to be joined to (even with Ben-Gan's method), the code in this article will take about three times as long to execute. For a millon nodes, that took about 3.5 minutes on my laptop. Considering that such a thing use to take about 2 days to run, I'm thinking that you might still be happy with this code. If you're not, then you need to come up with a more efficient method of splitting the SortPath with something that doesn't join directly to the VARBINARY(MAX) SortPath as the code currently does with the HTally Table.

Conclusion

Heh… this article is already long enough. Perhaps another song will do. Ready? SING IT WITH ME!

Sung happily to the tune of 'Row, row, row your boat'.

No, no, no you don't,

RBAR through the paths,

Tally, Tally, Tally, Tally

Set-Based saved my…

... hierarchies. 😉

Acknowledgements

This article would not have been possible without some of the knowledge I've gained from three individuals in particular either directly or indirectly.

First, and of course, when you say "hierarchies in SQL" or "Nested Sets", you have to stand up and salute Joe Celko for the work that he's done on the subject over the years. He literally wrote the book on the subject.

Without the brilliant formulas that Adam Machanic came up with that I used in this article, I'd still be looking for a way to quickly convert an Adjacency List to Nested Sets. All I did was tweak the method for performance using a Tally Table and explain why his formulas work so very well. Please visit the same article that I did way back in early 2009 at the following URL.

http://sqlblog.com/blogs/adam_machanic/archive/2006/07/12/swinging-from-tree-to-tree-using-ctes-part-1-adjacency-to-nested-sets.aspx

Last but not least, I don't know who actually wrote the very first article I ever saw on the use of Numbers Tables (I call them Tally Tables), but thank you for making my life a whole lot easier.

Thank for listening, folks.

--Jeff Moden

p.s. There's actually one more "miracle" that we can do… although Nested Sets will always have a purpose, we can make Nested Sets virtually obsolete for calculation purposes. See how in Part 2 of "Hierarchies on Steroids".

¹ "RBAR is pronounced "ree-bar" and is a "Modenism" for "Row-By-Agonizing-Row"

© Copyright Jeff Moden, 06 Oct 2012, All Rights Reserved