This was an interesting problem that someone posted online. How can I take this:
0000000000001000000000000000000000000010
and convert it to:
8000002
If you’re not following, the top is a binary representation and the bottom is hex. A few other examples would be:
Binary: 1111 Hex: F
Binary: 10000 Hex: 10
These examples are interesting in T-SQL to solve. There are two ways to represent data in binary in T-SQL: string or numeric. Numeric is a large, long string essentially, as our conversion would need to add up the values of each “number” in the string based on some power of two.
I found a function from Mark Rasmussen, but I like to try and do things without a looping in T-SQL, so let me try. First, we need to get an algorithm and then implement it.
Note: This is only designed for positive numbers. If you need negative numbers, there is a comment in the discussion that adds the capability
The Algorithm
The basic method for converting a binary number to a hex for me is to convert the number to base 10 (decimal) and then use the CONVERT() function to cast this as varbinary. This will return the hex equivalent. For example, I can do this:
SELECT hexvalue = CONVERT(varbinary(100), 15) ;
I then get this:
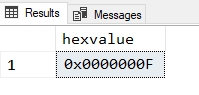
That works fine. If you test other values, you'll get the correct hex value. That means I really need to convert binary to decimal and let SQL Server handle the rest.
Converting a binary value to a decimal involves looking at the placement of each number in the binary data and converting that to a power of 2. I do this from right to left for counting, with each place representing a specific power of 2 starting with 0. This means that the first digit (rightmost) is 2^0, which is 1. I can multiple the value of the digit by 2^0 to get the value. In a table, this means:
| Rightmost binary digit | Decimal value |
| 0 | 0 * 2^0 = 0 |
| 1 | 1 * 2^0 = 1 |
That's easy. If I continue moving right to left, each place increases the power of two by one. This means that the value of 10111 is computed as follows. I'll go from right to left in the table.
| Binary digit | Decimal value |
| 1 | 1 * 2^0 = 1 |
| 1 | 1 * 2^1 = 2 |
| 1 | 1 * 2^2 = 4 |
| 0 | 0 * 2^3 = 0 |
| 1 | 1 * 2^4 = 16 |
The result is the sum of the decimal values or 23. With that, I can start to build a function that doesn't use a loop.
Setting Up a Test
I like to use repeatable testing when I'm building a function. It means that as I want to test different values, I can do so easily, without relying on my human mind to not make a mistake. I'm a fan of the tsqlt framework, and it works well here. Let's set up a test. First, I want to create a stub function I can call in my test. I'll do this with this code:
CREATE OR ALTER FUNCTION dbo.BinaryToHex( @bin VARCHAR(64)) RETURNS VARBINARY(100) AS BEGIN DECLARE @return VARBINARY(100); SET @return = CONVERT(VARBINARY(100), 15) RETURN @return END
Now we can set up a test. I'll do this by creating my procedure and adding the assemble section. This involves first creating two tables where I can test multiple values. The next step is to create some values that I can use. I had to use a calculator for a few of these, but I want a range of values. I can alter this over time to increase the number and variety of cases that I cover. Note that in deciding on the values, I had to do some work in SQL Server to see how many zeros were used with varbinary. I could insert a converted decimal to get the answer.
Here is the opening of the procedure.
CREATE OR ALTER PROCEDURE tsqltests.[test convert binary to hex]
AS
BEGIN
--Assemble
CREATE TABLE #Expected( hexvalue VARBINARY(100))
CREATE TABLE #Actual( hexvalue VARBINARY(100))
INSERT #Expected (hexvalue)
VALUES (0x000000000000002)
, (0x00000000000000A)
, (0x00000000000000F)
, (0x0000000000000FF)
, (0x000000008000002)
Next is the act section, where we get the results of our code. I use a simple INSERT statement here for each case. Again, expanding this means updating the inserts above and below.
-- Act
INSERT #Actual (hexvalue) SELECT dbo.BinaryToHex('10')
INSERT #Actual (hexvalue) SELECT dbo.BinaryToHex('1010')
INSERT #Actual (hexvalue) SELECT dbo.BinaryToHex('1111')
INSERT #Actual (hexvalue) SELECT dbo.BinaryToHex('11111111')
INSERT #Actual (hexvalue) SELECT dbo.BinaryToHex('0000000000001000000000000000000000000010')The last part of the test is to check the two tables against each other.
-- Assert
EXEC tsqlt.AssertEqualsTable
@Expected = N'#expected'
, @Actual = N'#actual'
, @Message = N'Incorrect conversion'
ENDIf we run the test now, it will fail as each call to the function will return the same value, and we have different input values. However, this gives us a test we can run many times as we develop our function. To run the test, we do so like this:
EXEC tsqlt.run 'tsqltests.[test convert binary to hex]'
Building a Function
Since I need to process a string, this feels like a place where a tally table works well. Let's start there and alter our function to use a tally table. I'll start with a short one that contains 100 numbers. We could have a binary number that has more digits, but that's good for now.
CREATE OR ALTER FUNCTION dbo.BinaryToHex
(@bin VARCHAR(MAX))
RETURNS VARBINARY(100)
AS
BEGIN
DECLARE @return VARBINARY(100)
;
WITH myTally (n)
AS
-- SQL Prompt formatting off
(SELECT n = ROW_NUMBER() OVER (ORDER BY (SELECT null))
FROM (VALUES (1), (2), (3), (4), (5), (6), (7), (8), (9), (10)) a(n)
CROSS JOIN (VALUES (1), (2), (3), (4), (5), (6), (7), (8), (9), (10)) b(n)
),
-- SQL Prompt formatting onThis gives me a set of numbers from 1 to 100. How can I use that? The first part of this is separating out each part of the binary number. Since I want to work right to left, I'll do this by reversing the string. I'll add a second CTE to separate the numbers, and since I know I'll be SUMming the values, I'll use that in the final query to set the return value.
CREATE OR ALTER FUNCTION dbo.BinaryToHex
(@bin VARCHAR(MAX))
RETURNS VARBINARY(100)
AS
BEGIN
DECLARE @return VARBINARY(100)
;
WITH myTally (n)
AS
-- SQL Prompt formatting off
(SELECT n = ROW_NUMBER() OVER (ORDER BY (SELECT null))
FROM (VALUES (1), (2), (3), (4), (5), (6), (7), (8), (9), (10)) a(n)
CROSS JOIN (VALUES (1), (2), (3), (4), (5), (6), (7), (8), (9), (10)) b(n)
),
-- SQL Prompt formatting on
binCTE (i)
AS (SELECT
CAST(SUBSTRING(REVERSE(@bin), n, 1) as BIGINT)
FROM myTally
WHERE n <= LEN(@bin))
SELECT @return = CONVERT(VARBINARY(100), SUM(i)) FROM binCTE
;
RETURN @return
;
ENDNote that I've use a WHERE clause in my second CTE to limit the values to those that match the length of the binary number. If I don't do this, I'll get errors in the SUBSTRING function.
The last part of this is to take each digit from the binary number and multiply it by a power of 2. I add this to the second CTE. The SELECT for the second CTE is shown here.
SELECT
POWER(CAST(2 AS BIGINT), n - 1)
* CAST(SUBSTRING(REVERSE(@bin), n, 1) AS BIGINT)
FROM myTally
WHERE n <= LEN(@bin))
Does It Work?
Let's see. I'll execute the test run once I've built the function. I see this:
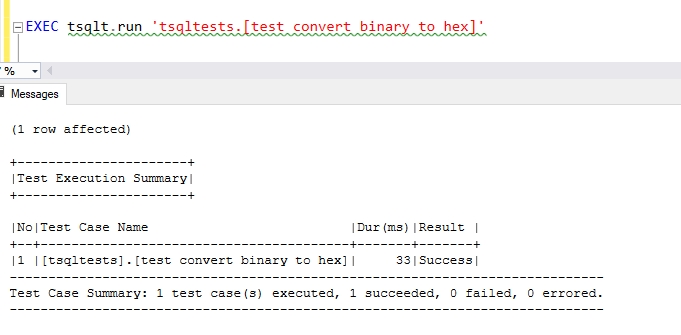
I had to experiment a bit to get the function working. Here's the result if I remove a zero from a couple of the inserts into the #expected table.
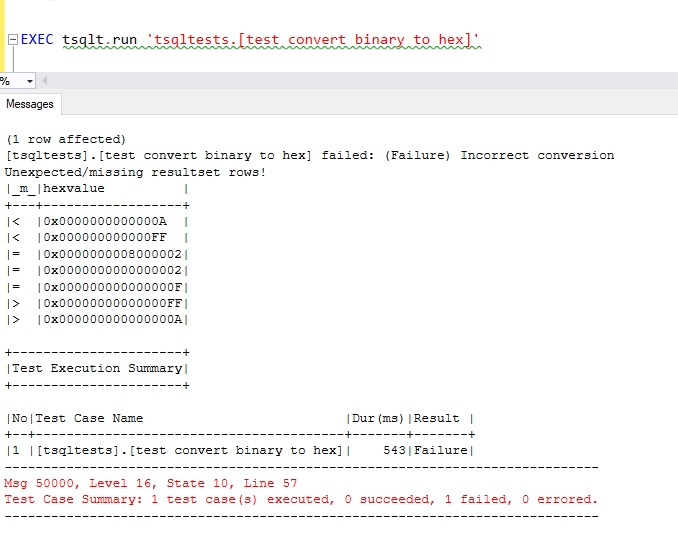
The results show that the #expected table (with the < in the results) are short zeroes. The #actual table shows what the function returned where the results matched #expected (with the =) or don't (with the >).
Conclusion
In this article, I wanted to show two main things. First, that it's fairly simple to convert binary numbers to hex with a function. You say how I built up an algorithm using a tally table. If you'd prefer the loop, you can read Mark's article (linked above).
The second thing I wanted to show was a little automated testing can be useful here, and it's not hard to set up. I used tsqlt to create a unit test that examines a few cases. I could easily add cases here, and I can push this into any automated continous integration area to ensure that this function is tested and doesn't regress if someone makes changes. While this is a little more effort to start than running a series of function calls and checking results in a calculator, over time this saves me from making changes to the UDF and forgetting to test some cases.

