This is Chapter 9 of my Data Mining articles. If you want to see the earlier chapters, you can read the previous articles in this series using the links below:
- An introduction to data mining
- Decision trees
- Clusters
- Naïve Bayes
- Neural Network
- Time series
- Microsoft Association
- Microsoft Sequence Cluster
There is not too much documentation about the Linear Regression Algorithm. Maybe because it is too simple. This article will explain the algorithm and then we will create an easy sample to show how it works.
The linear regression is an algorithm used to predict one variable based in another one. For example, we can predict the gold prices over the time, the relationship between tobacco smoking and the mortality, the temperature and the number of people with flu.
The relationship follows a behavior similar than a line. That is why it is called linear regression.
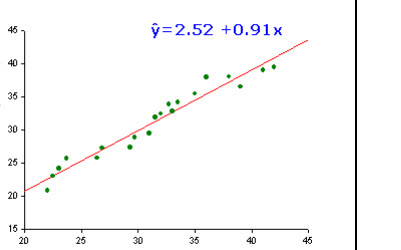
We need some samples of data for this model and an input variable to estimate the dependent variable. Here you have an example:
Getting Started
In this sample, we are going to predict the price of a house based on the square meter size of the houses. Let say that we are selling houses and that we have a table with the meters and the price of the house.

The table contains the following information:
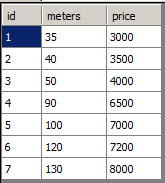
Meters are the square meters (m2) and the price contains the price according to m2. For example, if the house has 35 m2, the price would be 3000 USD, if the house has 40 m2 the price will be 3500 USD. In order to create the table with data, you can use this script:
USE [AdventureWorksDW2012]
GO
/****** Object: Table [dbo].[HousePrices] Script Date: 5/2/2014
5:09:15 PM ******/SET ANSI_NULLS ON
GO
SET QUOTED_IDENTIFIER ON
GO
CREATE TABLE [dbo].[HousePrices](
[id] [smallint] NOT NULL,
[meters] [smallint] NULL,
[price] [smallint] NULL,
CONSTRAINT [PK_HousePrices] PRIMARY KEY CLUSTERED
(
[id] ASC
)WITH (PAD_INDEX = OFF, STATISTICS_NORECOMPUTE = OFF, IGNORE_DUP_KEY =
OFF, ALLOW_ROW_LOCKS = ON, ALLOW_PAGE_LOCKS = ON) ON [PRIMARY]
) ON [PRIMARY]
GO
INSERT [dbo].[HousePrices] ([id], [meters], [price]) VALUES (1, 35, 3000)
INSERT [dbo].[HousePrices] ([id], [meters], [price]) VALUES (2, 40, 3500)
INSERT [dbo].[HousePrices] ([id], [meters], [price]) VALUES (3, 50, 4000)
INSERT [dbo].[HousePrices] ([id], [meters], [price]) VALUES (4, 90, 6500)
INSERT [dbo].[HousePrices] ([id], [meters], [price]) VALUES (5, 100, 7000)
INSERT [dbo].[HousePrices] ([id], [meters], [price]) VALUES (6, 120, 7200)
INSERT [dbo].[HousePrices] ([id], [meters], [price]) VALUES (7, 130, 8000)Now, we want to predict the price if we have the number of square meters using the table created. To do this, we are going to add the table to the AdventureWorks model used in earlier chapters.
1. To add the table, go to the solution Explorer and select the Adventureworks DataSource View. In the design pane right click and select the Add/Remove Tables and add the HousePrices table and save the project.
2. In the Solution Explorer, in the mining structure right click and select New Mining Structure. You will have the Data Mining Wizard. Press next.
3. In the Create the Data Mining Structure, select the Microsoft Linear Regression.
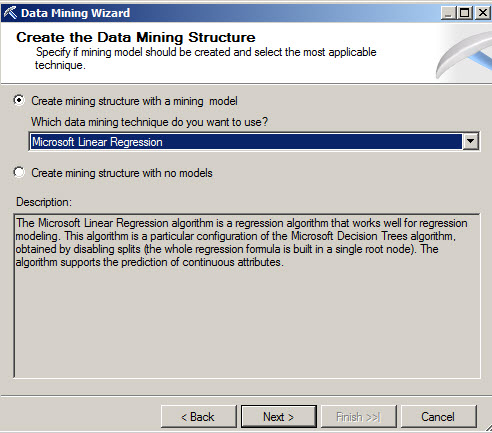
4. In the select Data Source View, select the Adventure Works Data Source.
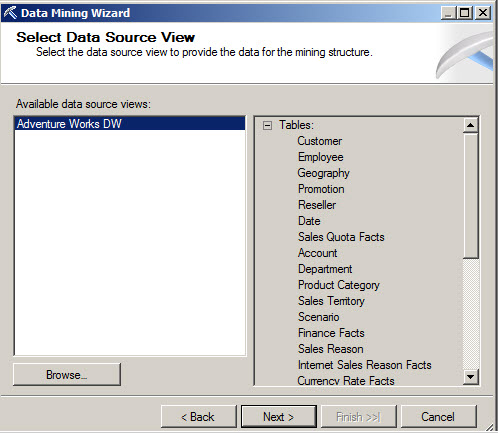
5. In the Specify Table Types, select the HousePrices. This is the table created with the prices per square meter.
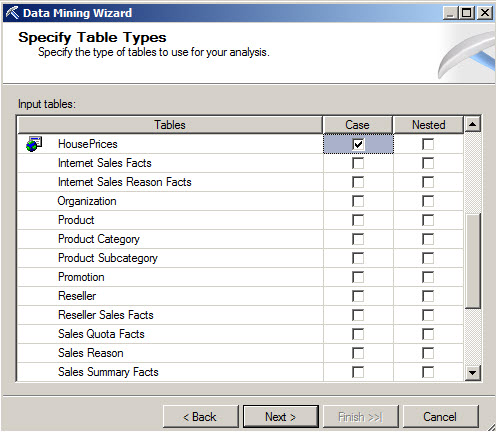
6. The key is the id used, the meters are going to be used as the input columns. Based on the square meters we are going to predict the price. The predicted column will be the price.
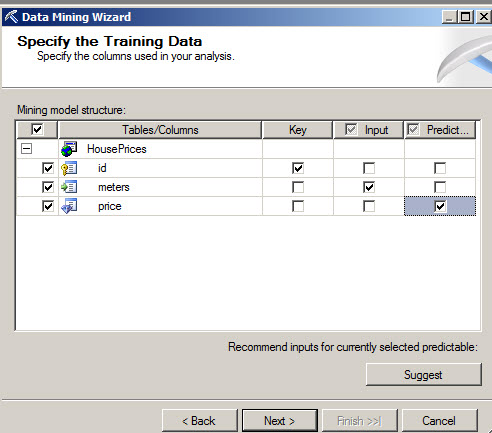
7. We will live the Content type with the default values.
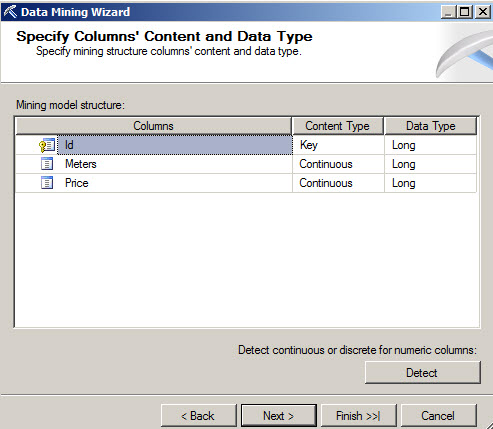
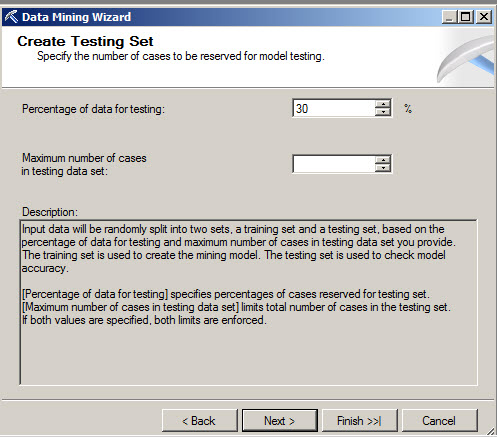
8. For the Create Testing Set we will use the default values.
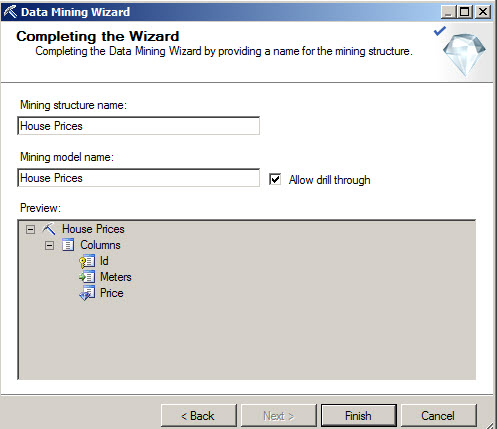
9. Finally, you can specify any name for the Structure and Mining Model. Press finish and compile the model like we did in ealier chapters.
10. Now we have the model created in step 9
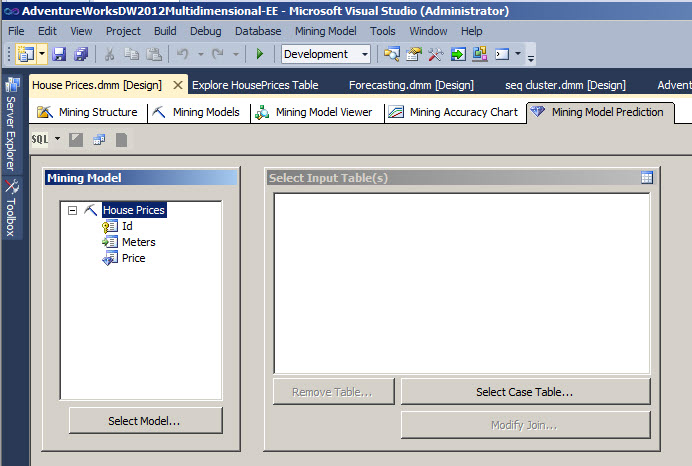
11. In the case table select the HousePrice Table and press OK.
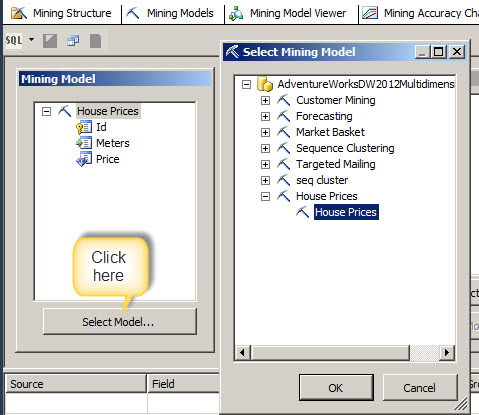
12. Make sure you are in Singleton Query mode.
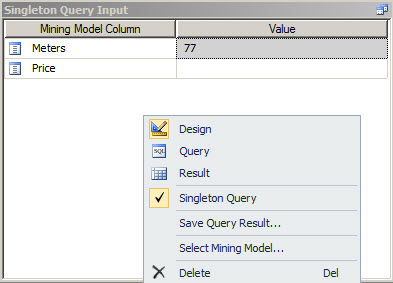
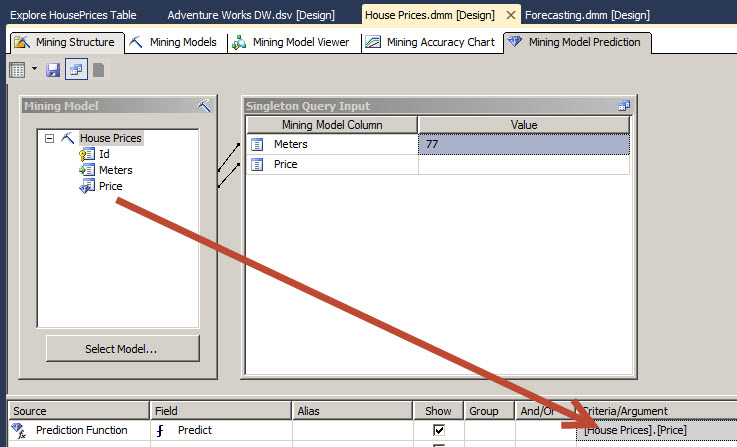
13. Now use a Prediction Function to predict the price. Drag and drop the Price as an argument of the function.
14. Now we are going to ask the model the price of 43 m2.
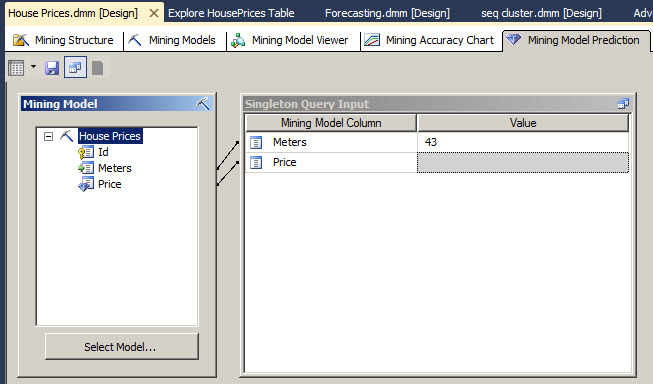
15. Go to the result.
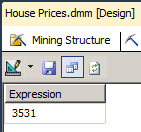
16. The price of 43 m2 is 3531 USD.
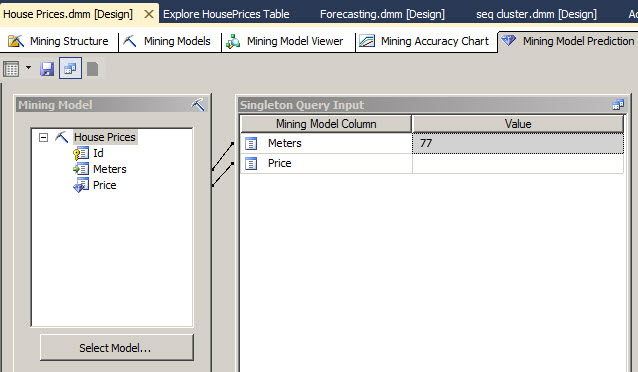
17. What is the price of a 77 m2 house?
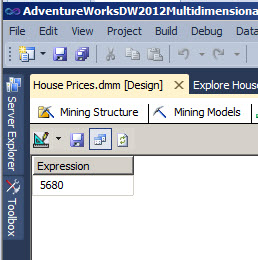
18. According to the model, 5680 USD.
Summary
In this lesson, we used the linear regression algorithm to estimate values according to a variable. We can estimate different statistics, prices using this algorithm. We just need some initial values and the algorithm will detect and estimate our results according to our input. In our sample we estimate the price of a house based on a the m2.

