By Steve Bolton
…………The last seven articles in this series of mistutorials on identifying outlying values in SQL Server database were clunkers, in the sense that the methods had many properties in common that made them inapplicable to the scenarios DBAs typically need them for. Chauvenet’s Criterion, Peirce’s Criterion, the Tietjen-Moore Test, the Generalized Extreme Studentized Deviate Test (GESD), Grubbs’ Test, the Modified Thompson-Tau Test and Dixon’s Q-Test are well-suited to the uses they were designed for, like hypothesis testing, but are difficult to apply to common SQL Server use cases like finding data quality problems in tables of several millions rows or doing exploratory data mining. Most of them require prior goodness-of-fit testing to verify that the underlying data follows a Gaussian “normal” distribution, i.e. a bell curve, without which they are invalid; many of the lookup tables they depend on are widely available but stop at just a few hundred rows at best, while calculating the missing lookup values for millions of cases can be exceptionally costly. Toss in other drawbacks of hypothesis testing that are often unstated these days (like the use of arbitrary confidence levels and misconceptions about probabilistic reasoning, which statisticians themselves raise frequently in their literature) and it appears that for most scenarios, DBAs would be better off sticking with the methods we kicked off the series with, Z-Scores and Benford’s Law. I’m only writing about these topics as an amateur, but the inapplicability of so many standard outlier identification methods to larger datasets makes me wonder if it the age of “Big Data”[1] doesn’t call for the devising of new means of detection. Thankfully, however, we haven’t by any means exhausted the means already available to us in the common statistical literature, without having to delve into research papers and academic journals and that sort of thing. I haven’t yet had a chance to discuss Interquartile Range because I’m trying to group the detection methods by the properties they have in common, but this particular one has little overlap with any of the others we’ve surveyed to date. It nevertheless performs relatively well and is applicable to a much wider set of use cases than any other means we’ve discussed since finishing up Z-Score a couple of months ago.
…………Interquartile Range has apparently been in use for so long and is so pervasive in academic research that the story of its origin is difficult to find in a cursory search, unlike the colorful histories of some of the lesser-known methods discussed in recent posts. In-depth research of this kind wasn’t really necessary for this week’s article because the calculations and concepts are easier than anything we’ve discussed to date.[2] The idea is fairly simple: instead of calculating a single center point for the whole dataset, we establish two boundaries known as the lower and upper quartiles encompassing the middle half of the values, so named because they are a quarter of the way (25 percent and 75 percent) from the edges of the dataset. The Interquartile Range is just another single measure of how dispersed data is around the center of the dataset, like the more familiar standard deviation and variance, except that it is less sensitive to outlying values (i.e., it is more “robust”). Computing it is trivial once we got the lower and upper quartiles, since all we have to do is subtract the former from the latter. Interquartile Range is apparently useful for other applications such as goodness-of-fit testing, but when used to find those aberrant data points we call outliers, it is usually accompanied by calculations of upper and inner fences. These are established by simply subtracting or adding 1.5 times the Interquartile Range from the lower quartile or doing the same with the upper quartile, except with 3 times the Interquartile Range. Using this test, any values falling outside these four “fences” are defined as outliers. The math in Figure 1 looks a lot more complicated than it really is, when all we’re really doing is a few modulos and simple divisions to get the lower and upper quartiles, then some simple subtraction and multiplication to establish the fence values. The most difficult part of the T-SQL code is probably the common table expression (CTE), which is trivial compared to some of the more difficult nested subqueries, UNPIVOT operations and windowing functions used in other recent tutorials.
Figure 1: Code for the Interquartile Range Procedure
CREATE PROCEDURE [Calculations].[InterquartileRangeSP]
@DatabaseName as nvarchar(128) = NULL, @SchemaName as nvarchar(128), @TableName as nvarchar(128),@ColumnName AS nvarchar(128), @PrimaryKeyName as nvarchar(400), @OrderByCode as tinyint = 1, @DecimalPrecision AS nvarchar(50)
AS
SET @DatabaseName = @DatabaseName + ‘.’
DECLARE @SchemaAndTableName nvarchar(400)
SET @SchemaAndTableName = ISNull(@DatabaseName, ”) + @SchemaName + ‘.’ + @TableName
DECLARE @SQLString nvarchar(max)
SET @SQLString = ‘DECLARE @OrderByCode tinyint,
@Count bigint,
@LowerPoint bigint,
@UpperPoint bigint,
@LowerRemainder decimal(38,37), — use the maximum precision and scale for these two variables to make the
procedure flexible enough to handle large datasets; I suppose I could use a float
@UpperRemainder decimal(38,37),
@LowerQuartile decimal(‘ + @DecimalPrecision + ‘),
@UpperQuartile decimal(‘ + @DecimalPrecision + ‘),
@InterquartileRange decimal(‘ + @DecimalPrecision + ‘),
@LowerInnerFence decimal(‘ + @DecimalPrecision + ‘),
@UpperInnerFence decimal(‘ + @DecimalPrecision + ‘),
@LowerOuterFence decimal(‘ + @DecimalPrecision + ‘),
@UpperOuterFence decimal(‘ + @DecimalPrecision + ‘)
SET @OrderByCode = ‘ + CAST(@OrderByCode AS nvarchar(50)) + ‘ SELECT @Count=Count(‘ + @ColumnName + ‘)
FROM ‘ + @SchemaAndTableName +
‘ WHERE ‘ + @ColumnName + ‘ IS NOT NULL
SELECT @LowerPoint = (@Count + 1) / 4, @LowerRemainder = ((CAST(@Count AS decimal(‘ + @DecimalPrecision + ‘)) + 1) % 4) /4,
@UpperPoint = ((@Count + 1) *3) / 4, @UpperRemainder = (((CAST(@Count AS decimal(‘ + @DecimalPrecision + ‘)) + 1) *3) % 4) / 4; –multiply by 3 for the left s’ + @PrimaryKeyName + ‘e on the upper point to get 75 percent
WITH TempCTE
(‘ + @PrimaryKeyName + ‘, RN, ‘ + @ColumnName + ‘)
AS (SELECT ‘ + @PrimaryKeyName + ‘, ROW_NUMBER() OVER (PARTITION BY 1 ORDER BY ‘ + @ColumnName + ‘ ASC) AS RN, ‘ + @ColumnName + ‘
FROM ‘ + @SchemaAndTableName + ‘
WHERE ‘ + @ColumnName + ‘ IS NOT NULL),
TempCTE2 (QuartileValue)
AS (SELECT TOP 1 ‘ + @ColumnName + ‘ + ((Lead(‘ + @ColumnName + ‘, 1) OVER (ORDER BY ‘ + @ColumnName + ‘) – ‘ + @ColumnName + ‘) * @LowerRemainder) AS QuartileValue
FROM TempCTE
WHERE RN BETWEEN @LowerPoint AND @LowerPoint + 1
UNION
SELECT TOP 1 ‘ + @ColumnName + ‘ + ((Lead(‘ + @ColumnName + ‘, 1) OVER (ORDER BY ‘ + @ColumnName + ‘) – ‘ + @ColumnName + ‘) * @UpperRemainder) AS QuartileValue
FROM TempCTE
WHERE RN BETWEEN @UpperPoint AND @UpperPoint + 1)
SELECT @LowerQuartile = (SELECT TOP 1 QuartileValue
FROM TempCTE2 ORDER BY QuartileValue ASC), @UpperQuartile = (SELECT TOP 1 QuartileValue
FROM TempCTE2 ORDER BY QuartileValue DESC)
SELECT @InterquartileRange = @UpperQuartile – @LowerQuartile
SELECT @LowerInnerFence = @LowerQuartile – (1.5 * @InterquartileRange), @UpperInnerFence = @UpperQuartile + (1.5 * @InterquartileRange), @LowerOuterFence = @LowerQuartile – (3 * @InterquartileRange), @UpperOuterFence = @UpperQuartile + (3 * @InterquartileRange)
–SELECT @LowerPoint AS LowerPoint, @LowerRemainder AS LowerRemainder, @UpperPoint AS UpperPoint, @UpperRemainder AS UpperRemainder
— uncomment this line to debug the inner calculations
SELECT @LowerQuartile AS LowerQuartile, @UpperQuartile AS UpperQuartile, @InterquartileRange AS InterQuartileRange,@LowerInnerFence AS LowerInnerFence, @UpperInnerFence AS UpperInnerFence,@LowerOuterFence AS LowerOuterFence, @UpperOuterFence AS UpperOuterFence
SELECT ‘ + @PrimaryKeyName + ‘, ‘ + @ColumnName + ‘, OutlierDegree
FROM (SELECT ‘ + @PrimaryKeyName + ‘, ‘ + @ColumnName + ‘,
”OutlierDegree” = CASE WHEN (‘ + @ColumnName + ‘ < @LowerInnerFence AND ‘ + @ColumnName + ‘ >= @LowerOuterFence) OR (‘ +
@ColumnName + ‘ > @UpperInnerFence
AND ‘ + @ColumnName + ‘ <= @UpperOuterFence) THEN 1
WHEN ‘ + @ColumnName + ‘ < @LowerOuterFence OR ‘ + @ColumnName + ‘ > @UpperOuterFence THEN 2
ELSE 0 END
FROM ‘ + @SchemaAndTableName + ‘
WHERE ‘ + @ColumnName + ‘ IS NOT NULL) AS T1
ORDER BY CASE WHEN @OrderByCode = 1 THEN ‘ + @PrimaryKeyName + ‘ END ASC,
CASE WHEN @OrderByCode = 2 THEN ‘ + @PrimaryKeyName + ‘ END DESC,
CASE WHEN @OrderByCode = 3 THEN ‘ + @ColumnName + ‘ END ASC,
CASE WHEN @OrderByCode = 4 THEN ‘ + @ColumnName + ‘ END DESC,
CASE WHEN @OrderByCode = 5 THEN OutlierDegree END ASC,
CASE WHEN @OrderByCode = 6 THEN OutlierDegree END DESC‘
–SELECT @SQLString — uncomment this to debug string errors
EXEC (@SQLString)
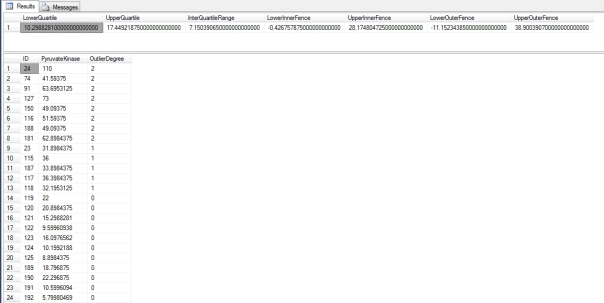
…………The code in Figure 1 basically follows the same format as that of other procedures I’ve posted in this series, for simplicity’s sake. The first five parameters allow users to test any column in any database they have access to, while the @DecimalPrecision enables them to avoid arithmetic overflows by manually setting a precision and scale appropriate to the column they’ve selected. As usual, the procedure is created in a Calculations schema; there are no brackets to handle spaces in object names, nor is there any validation or SQL injection code. As with past procedures, uncommenting the next-to-last line allows users to debug the dynamic SQL; I also provided a second debugging point of the same kind midway through the procedure, for testing the inner calculations. The @OrderByCode I’ve used in previous tutorials also returns, with the same values as usual: value #1 and #2 allow users to order by the primary key ascending and descending, while #3 and #4 do the same for the ColumnName and #5 and #6 order the results by the OutlierDegree column. As depicted below, the OutlierDegree column allows for a range of values depending on how much a particular data point deviates from the norm, not merely a Boolean yes-no flag like we’ve seen in many hypothesis-testing based methods. Note that the results also include the Interquartile Range, fence values and quartiles used to test each data point.
Figure 2: Results for the Interquartile Range Procedure on the PyruvateKinase Column
EXEC [Calculations].[InterquartileRangeSP]
@DatabaseName = N’DataMiningProjects‘,
@SchemaName = N’Health’
@TableName = N’DuchennesTable‘,
@ColumnName = N’PyruvateKinase‘,
@PrimaryKeyName = N’ID’,
@OrderByCode = 6,
@DecimalPrecision = N’38,21′
…………The test in Figure 2 was performed on the Pyruvate Kinase column of a 209-row dataset on the Duchennes form of muscular dystrophy, which I downloaded from the by Vanderbilt University’s Department of Biostatistics and converted to a SQL Server table. For the sake of consistency, I’ve stress-tested outlier detection methods that might have performance issues on the first float column of the Higgs Boson Dataset, which is made publicly available by the University of California at Irvine’s Machine Learning Repository and now occupies almost 6 gigabytes of my practice database. On average, the procedure took about 18-and-a-half to 19 minutes to run against the 11 million rows of that dataset on my poor beat-up semblance of a development machine, as compared to about 3 minutes for the Z-Score procedure I posted earlier in the series. The addition of a non-clustered index on the column improved things a little – as long as I included the clustered primary key, but the execution plans were still too large to post; suffice it to say that they consisted mainly of parallel non-clustered index Seeks with some expensive Sorts, plus a lot of Spools that had inconsequential costs. Perhaps a columnstore index would help things, but I’ve been unable to upgrade yet to SQL Server 2014, where many of the restrictions that once hobbled the feature have been relaxed.
…………Since Z-Scores perform better and can be used in conjunction with any outlier threshold that end users choose, they remain enthroned as the most widely applicable detection method we’ve yet discussed. Nonetheless, Interquartile Range is more likely to be of use to DBAs than the hypothesis testing-based means that took up the middle segment of this series. The calculations are simple to code and perform, the concepts aren’t that hard to explain to database users and perhaps best of all, we’re not limited to using just a Gaussian bell curve. That also means we don’t have to do preliminary goodness-of-fit testing, which is so often omitted by careless researchers. One of the Wikipedia articles I found the formula at mentions it being used in conjunction with Cauchy and Laplace distributions, although not necessarily in its capacity as an outlier detector.[3] It can even be adapted for double duty as a goodness-of-fit test. In and of itself, it constitutes an alternate measure of dispersion that can be used in place of standard deviation and variance. The scenarios in which such a substitution would prove useful include ones where a measure less likely to be altered by outlying values is called for. The same property might make it more appropriate than Z-Scores when there is a real need for a more conservative test for outliers. Another plus in its favor is the fact that it also measures the degree of membership in the set of outliers on a scale, rather than merely flagging it as many hypothesis-testing methods do; furthermore, those methods have numerous other restrictions on the number and types of inputs, outputs and calculation methods that make them unsuitable for most SQL Server tasks, like recursive deletion with Chauvenet’s Criterion and the inability of Dixon’s Q-Test to identify more than one outlier per dataset. Moreover, the fence and quartile values are trivial to return once they’ve been calculated and constitute global measures in their own right.
…………I have yet to try Cook’s Distance and Mahalanobis Distance, but I have high hopes that they too will prove to be useful additions to the toolbelts of SQL Server data miners and DBAs. I hope to use both as a springboard into a much longer and more difficult, albeit worthwhile, series a few months down the line, Information Measurement with SQL Server. Before delving into the difficult math that underpins distance-based metrics of that kind, however, I will give a brief overview of how to use Reporting Services to find outliers the easy way: by the naked eye. Finding outliers is not always that straightforward, but in many cases all we need to do is spot them in a histogram or scatter plot, where they sometimes stand out like sore thumbs. They are sometimes also glaringly obvious in the diagrams produced by the Clustering algorithm in SSDM, which I may give a quick refresher on, based on my last tutorial series, A Rickety Stairway to SQL Server Data Mining. As we will see, scaling up visual detection methods of this kind to meet the size of SQL Server databases is the primary challenge, just as their size stretches beyond the ordinary bounds of hypothesis testing. The pervasiveness of the size issue makes me wonder, once again, if it might not be worthwhile to devise new scalable methods of outlier detection to complement the ones already in common use today.[4]
[1] This buzzword is a lot like the overused term “globalization.” Unlike with statistics and data mining, I have real expertise in foreign policy history, and can say definitively that globalization has been going on for millennia; the only difference is that it has accelerated in recent decades. Likewise, the amount of Data the human race has to process is always getting Bigger; it’s just getting Bigger at a faster pace these days.
[2] I retrieved the formulas from the most convenient sources, the Wikipedia pages “Outlier” and “Interquartile Range” at http://en.wikipedia.org/wiki/Outlier and http://en.wikipedia.org/wiki/Interquartile_range respectively. I also tested the procedure against some of the examples provided there. Also see National Institute of Standards and Technology, 2014, “7.1.6. What are Outliers in the Data?” published in the online edition of the Engineering Statistics Handbook. Available online at the web address http://www.itl.nist.gov/div898/handbook/prc/section1/prc16.htm
[3] IBID.
[4] While writing this series I encountered an interesting suggestion by Will G. Hopkins, the writer of one of the best plain English explanations of statistics available online today: “Here’s something challenging for the real lovers of numbers. The mean ± SD encloses 68% of the data on average for a normally distributed variable. So if you want to use a percentile range that corresponds to the mean ± SD, what should it be? Answer: 16th-84th. If I had my way, this measure would replace the interquartile range. We could call it the standard percentile range…” I could write code for this easily, but didn’t bother because the series already features too many outlier identification methods that are dependent on a normal distribution. Nor would it necessarily do anything to help with the scaling problem I mentioned above. It does illustrate, however, how we’re not limited to just using tried and true measures and can devise new ones as needed, if they are appropriate to the contexts at hand. See Hopkins, Will G. 2013, “Percentile Ranges,” published at the website A New View of Statistics and available at the web address http://www.sportsci.org/resource/stats/percentile.html