by Steve Bolton
In the last installment of this series of self-tutorials on SQL Server Data Mining (SSDM), A Rickety Stairway to SQL Server Data Mining, Algorithm 3: Decision Trees, I glossed over an algorithm that built upon the data mining methods touched on in my first two posts, Naïve Bayes and Linear Regression. This week’s topic also branches off from Linear Regression, but in a different direction than Decision Trees. Thankfully, it does have some of the same strengths as its distant cousin, in that it can accept both Discrete and Continuous data. As I discuss in more depth in A Rickety Stairway to SQL Server Data Mining, Part 0.0: An Introduction to an Introduction, the distinction between these two Content types is crucial but possibly unfamiliar to relational DBAs, who may not be used to distinguishing data by its meaning. A column labeled as Discrete represents a state or class, such as a GUID or database name, whereas a Continuous column holds data that represents a numeric range with an order and rank; the latter can be treated as Discretized, meaning that the range is broken up into buckets that have no order or rank, so that the ranges are treated as states with no relationship to each other. The Discretized Content type is a necessary evil for algorithms that don’t accept Continuous values, but Logistic Regression can fortunately process both. Books Online (BOL) doesn’t mention that it can also take the special Cyclical and Ordered types although the columns can be set to both in SQL Server Data Tools (SSDT) when Logistic Regression is the selected algorithm – which doesn’t make much of a difference, since they are treated as Discrete anyways by every algorithm except Sequence Clustering. A single input attribute of the Key Content type is required for every mining model, as usual; the only departure from the norm is that Logistic Regression can only accept the Table type as inputs rather than predictable output columns. Nested tables are an advanced topic that we won’t be discussing until we tackle the Sequence Clustering and possibly the Association Rules algorithms – thanks in part to my misadventure with them in A Rickety Stairway to SQL Server Data Mining, Part 0.2: How to Dig Out of a Data Mining Cave-In.
Logistic Regression is relatively simple to grasp, once you understand the explanations for its Linear cousin in A Rickety Stairway to SQL Server Data Mining, Algorithm 2: Linear Regression. The easiest way to visualize Linear Regression is a scatter plot, in which the line drawn through the graph represents some sort of comparison of the data points, like a sophisticated average. Decision Trees is a bit more complex in that its regression trees have lines that meet at angles, in order to deal with non-linear data; from there, we can extrapolate the data into formats similar to another common visualization method, flow charts. Logistic Regression deals with data that is non-linear in a different way, or which is bounded, such as percentages that can only range from 0 to 100. The answer for both dilemmas is to weight the outputs so that they can approach but never cross beyond the limits, a solution that is also applicable to functions that produce curved rather straight results. The simplest way to explain it is that it forms an S-curve rather than a straight line in a scatter plot. Since the straight and crooked lines in Linear Regression and Decision Trees keep going, they are not as well-suited for predicting specific outcomes the way Logistic Regression is; this feature makes it useful for a wide range of applications in which the likelihood of specific outcomes must be compared. Economic forecasting, political polls, medical diagnosis, document classification and demographic prediction of customer choices are among the most popular uses for Logistic Regression for that reason.[ii] It is apparently not as valuable for analyzing data that naturally follows a linear pattern, as can be expected.
It is also useful for smoothing out exponential growth curves, which can be grossly unreliable when extrapolated beyond their original data. In fact, Alphonse Quetelet (1795-1874) and his protégé Pierre-François Verhulst (1804-1849) developed it in the 19th Century to correct the wild estimates of population growth made by Rev. Thomas Malthus (1766-1834) in his classic treatise, “An Essay on the Principle of Population.” In A Rickety Stairway to SQL Server Data Mining, Part 0.1: Data In, Data Out I made the controversial case that cutting edge math, like the hard sciences it often serves, is a very valuable tool that is also quite dangerous when not kept within its proper bounds; some of the most brilliant minds in both fields have been hobbled by severe mental illness or worse yet, put their talents in service of really boneheaded philosophies which were sometimes even reprehensible. As I touch on in the Linear Regression tutorial, the man most responsible for the development of that algorithm was Sir Francis Galton (1822-1911), a racist who invented the junk science of eugenics that later inspired Hitler. The history of this week’s algorithm is reversed, in that Quetelet and Verhulst (who were aided by parallel work on logistic functions by chemists researching autocatalytic reactions) were apparently sober-minded and decent men who corrected the thinking of a particularly bad philosopher.[iii] Malthus contended that the living standards of the human race could never advance in tandem with population growth because “Population, when unchecked, increases in a geometrical ratio, Subsistence, increases only in an arithmetical ratio.” Yet the entirety of his thesis was being disproved as he wrote it, because Europe was entering a period of rapid growth of both population and living standards thanks to the technological improvements of the Industrial Revolution. The critical error Malthus made was that he only considered men as mouths to feed, not as hands that could be put to work to make more food; in truth, technological growth is dependent upon population growth, because the tinkerers of the 19th Century and the scientists of the 21st alike would not be able to invent anything if other workers did not provide them food, power and many other services. Like many of the Enlightenment philosophers, Malthus was a dangerously unbalanced thinker who personified Oscar Wilde’s famous quip, “A cynic is a man who knows the price of everything, and the value of nothing.” Throughout this series I have always given some kind of disclaimer that I’m a novice when it comes to statistics, but I do have some real expertise in demographic and economic history, all of which has disproven everything Malthus ever wrote; even in our day, we see the fastest population growth in the poorest regions of the planet and baby busts in the commercialized countries of the West, thanks to sharp differences in culture. Many of the equations used by today’s demographers fail for the same reasons that many of the calculations of our economists fail, because they are put in service of Ivory Towers that have no basis in reality. A critical example of this is the influential report of the Club of Rome in 1972, which made all sorts of wild doomsday predictions about the planet’s natural resources running out, which turned out to be patently false. It was one of the greatest blunders in the history of statistics, put in service of one of the all-time greatest blunders in the history of the Enlightenment. The most positive development to emerge from these false ideas was Logistic Regression, which was developed to correct some of Malthus’ errors. This is yet another lesson that reasoning is much more important to good decision-making than math; data mining is a powerful tool with a lot of exciting potential, but without the kind of context math and the hard sciences can never provide, it may be useless or even dangerous. If either the reasoning or the evidence that is fed into data mining algorithms is garbage, we’ll get garbage out as the saying goes, regardless of how sophisticated or well-reasoned our calculations are after that point.
Assuming our foundation in reason is solid, we can use the building blocks of statistics as a ladder to Truth rather than constructing a meaningless Ivory Tower. Microsoft’s implementation of Logistic Regression uses Z-scores, a standard building block in statistics, to normalize the values of the inputs, so that columns with different ranges can still be compared to each other. Z-scores are a couple of levels higher than an ordinary average in sophistication. To construct them, you first calculate a Variance by subtracting the mean from each number in a dataset, then square them to get rid of negative values that might throw off the calculations, then divide the results by the number of data points minus one. Standard deviation is just the square root of the variance. Z-scores are a level above that, in that they compare a specific data point against the average and divided by the standard deviation, in order to examine how a particular value is relate to the rest of the dataset. Microsoft’s documentation has the precise formulae, which make some small adjustments for missing values and takes prior probabilities into account when dealing with Discrete data. Perhaps because it fairly old and well-known, there seems to be less academic research and fewer innovations with Logistic Regression than the rest of Microsoft’s nine algorithms. Microsoft’s version implements one of the few refinements, multinomial regression, in which more than two outputs states are possible. Some other refinements include Conditional Logistic Regression and the Proportional Odds model of Ordinal Logistic Regression, which are beyond the scope of this topic. One of the key differences between types of Logistic Regression is how their effectiveness is validated rather than how the results are calculated; this is not the case with its cousin Linear Regression, where validation is a simpler matter.[iv] The documentation mentions that users can retrieve the coefficients returned by SSDM to test their own methods of “goodness of fit,” but cautions that “the coefficients that are created as part of a logistic regression model do not represent odds ratios and should not be interpreted as such.”
The relative simplicity of the algorithm itself is mirrored by the plainness of its parameters. As usual, we won’t be setting the MODEL_EXISTENCE_ONLY and NOT_NULL flags, since our data has no nulls and we have no incentive to rob our data of meaning by reducing it to a dichotomous choice between Missing and Existing states. Unlike its cousin Decision Trees, Logistic Regression has no parameters that enable us to control the feature selection going on under the hood, except for the usual MAXIMUM_INPUT_ATTRIBUTES and MAXIMUM_OUTPUT_ATTRIBUTES that we’ve covered before. The Interestingness Score is used for Continuous attributes and can be retrieved from the model after processing, while Shannon’s Entropy, Bayesian with K2 Prior and Bayesian Dirichlet with Uniform Prior (BDE) are used for Discrete values, which is pretty much the same script that SSDM follows for the rest of its algorithms. The MAXIMUM_STATES parameter we used previously in A Rickety Stairway to SQL Server Data Mining, Algorithm 1: Not-So-Naïve Bayes also returns for an encore with Logistic Regression. The only other parameters seem to duplicate other functionality already included with all mining structures. The algorithm allows you to specify a HOLDOUT_PERCENTAGE, which seems to be equivalent to the HoldoutMaxPercent property each mining structure has. As usual, we will leave the latter at its default value, which reserves 30 percent of the cases for each model for training purposes. Like the mining structure property HoldoutSeed, the model parameter HOLDOUT_SEED adjusts the random number generator that selects cases out of that 30 percent for training. We’ll leave the latter at its default of zero, which means that the seed will be generated from the name of the mining model itself. In other algorithms aside from Logistic Regression’s cousin, the Neural Network algorithm, the seed is generated from the mining structure instead when HoldoutSeed is left at its default of zero. The number of cases selected for training is limited either by HOLDOUT_PERCENTAGE or SAMPLE_SIZE, whichever is lower. The latter places as absolute limit on the number of cases and defaults to 10,000, in contrast to its closest relative in the mining structure properties, HoldoutMaxCases, which defaults to 0 and behaves slightly differently. The point of having these parameters is to allow comparisons between mining models within the same structure, depending on the data used to train it. This is of more importance with the Neural Network algorithm, which is basically an enhanced version of Microsoft’s implementation of Logistic Regression, so we’ll experiment with these parameters in the next tutorial.
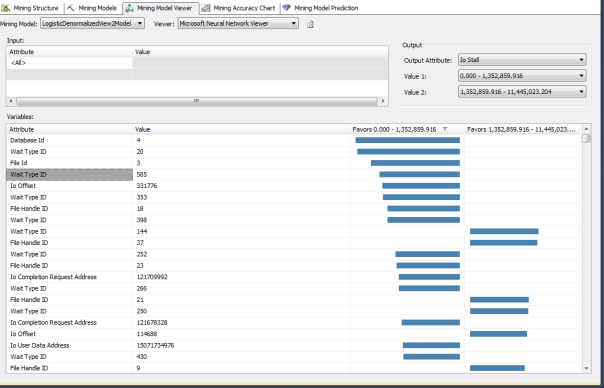
If we had to deprive one of Microsoft’s algorithms of parameters to tweak performance, Logistic Regression would be the ideal candidate, since all three mining structures were processed in record time. As discussed in more detail in post 0.2 and the tutorials on Naïve Bayes and Linear Regression, we’re using data derived from three days of polling the system views dm_exec_query_stats, dm_io_pending_io_requests, dm_io_virtual_file_stats, dm_os_performance_counters, dm_os_wait_stats and sp_spaceused every minute, which deliberately caused IO pressure in order to study the topic further. These tutorials have basically stuck with the same schema outlined in post 0.2, except that we’ve cut back to comparing mining structures built on three denormalized views comparing a parent RecordTable of time measures, dm_io_pending_io_requests, dm_io_virtual_file_stats and dm_os_performance_counters vs. sp_spaceused, dm_os_wait_stats and dm_exec_query_stats respectively. We’ve also cut out a few useless columns along the way, such as some measures of Common Language Runtime (CLR) function activity in the third structure. The first structure, in which the central table is sp_spaceused, had 142,080 rows but took just a minute and five seconds in this week’s trials. The structure built around dm_os_wait_stats took just a minute and a half to process 7,684,160 rows. The third mining structure took longer at 9:32 to process 3,887,072 rows (well, 70 percent of that number since 30 percent were reserved for training as usual), probably because dm_exec_query_stats returns many more columns than the tables the other two structures were built around. The figures for all three were much better than the processing times for nearly identical structures in the last three tutorials, which sometimes took hours depending on how the parameters for each algorithm were set. I received one cardinality reduction warning for the second mining structure and six with the third, which means that the MAXIMUM_STATES threshold could be raised in order to return calculations based on less popular input states. Tweaking this parameter entails a trade-off between performance and the quality of results, but there are no guarantees when altering this or any other parameter for any algorithm that the trade-off won’t turn into a devil’s bargain: in data mining we always face the constant threat of overfitting, in which we sacrifice performance in return for information glut. At best, that means sorting through clutter – in which case we have to mine the mining results themselves, so to speak – or at worst, false or misleading associations. Since the performance of the models was so encouraging I set the MAXIMUM_STATES threshold to zero for the mining models in the second and third structures, thereby allowing SSDM to include all of the input states in the results and eliminating the cardinality warnings. Processing time increased to 3:16 on the model for the second structure and 22:44 on the single model in the third structure. In return, we received a much longer list of results for certain comparisons; that required more time to sift through the model results but paid off by drawing out relationships for measures that we’re particularly interested in but which have been relatively absent in the past, such as those for WaitTypeID. Figure 1 shows many more links between IOStall and specific states of important input columns like WaitTypeID, DatabaseID and FileHandleID than we’re accustomed to seeing with other algorithms, but it really doesn’t do it justice: using the scrollbar reveals about a hundred more relationships, many of them involving other states of the key measure WaitTypeID.
Figure 1: Some Interesting Output for the Second Mining Structure in the Neural Network Viewer
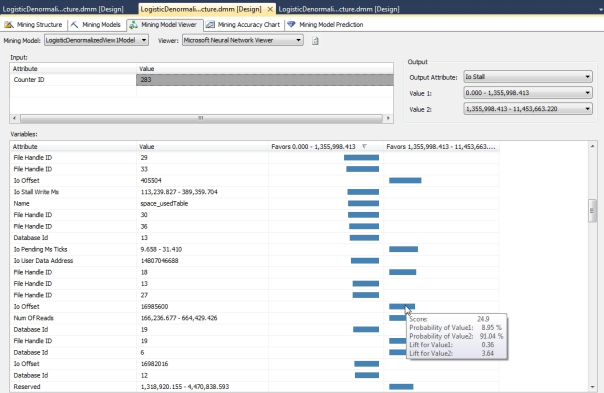
There is no Dependency Network tab to act as a convenient starting point in our visualization workflow. Logistic Regression uses the Neural Network Viewer, since it is basically a stripped-down version of that algorithm, but it has no additional tabs, nor does it support drillthrough to view the mining structure cases. Nevertheless, the single visualization technique SSDM provides is quite powerful. It operates similar to the Attribute Discrimination tab in the Naïve Bayes Viewer we discussed a few weeks back, except that instead of using the Attribute, Value1 and Value2 dropdowns to select a particular output and a range to test, you select one or more input attributes and a single value in the Input grid, then use the Output Attribute, Value1 and Value2 dropdowns to compare them against particular ranges of a predictable column. The result grid at the bottom of the viewer will display a list of other input attributes paired with particular values and display a bar chart indicating how strongly the cases support either Value1 or Value2. For example, in the graphic below we see some of the output when a single value for CounterID is compared against a range of IOStall values:
Figure 2: Comparison of One CounterID State vs. a Range of IOStall Values
There is no Mining Legend in the Neural Network Viewer, but you can still hover over a particular bar to view stats like the scores and probability comparisons. The higher the lift value associated with a particular output, the more useful the results are likely to be; SSDM can calculate this because we already know whether or not our cases fit the estimates generated from the training data.[v] The Viewer itself is much more useful and easy to interpret than many of the visualization tools we’ve surveyed to date – which is a good thing, because Logistic Regression seems to return more complex results. Its output is equivalent to a Neural Network without a hidden layer, which means that it shares pretty much the same structure of metadata, minus the middle of the network of course. As you can see from Figure 3, there are many more NODE_TYPE values for Logistic Regression than we’ve seen with previous algorithms, precisely because it is calculated like a stripped-down version of a neural net, which can be really intricate.
Figure 3: Metadata for Logistic Regression (adapted from Books Online as usual)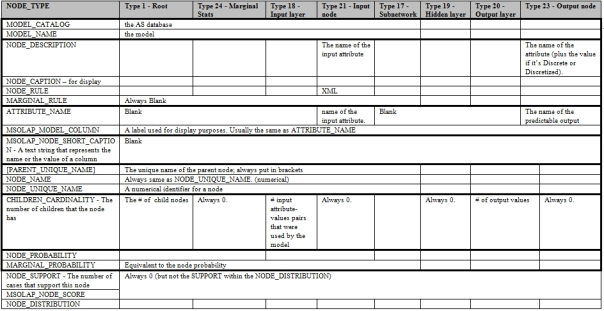
One of the difficulties of using the Generic Content Tree Viewer to dig down into the stats used by SSDM’s visualization tools is that the data difficult to interpret, but in the case of Logistic Regression and neural nets, it becomes maddeningly complex. As usual, we’re dealing with a denormalized table with columns that can vary in their meaning depending on the NODE_TYPE, as well as the nested table in the NODE_DISTRIBUTION column, in which the standard columns ATTRIBUTE_NAME, ATTRIBUTE_VALUE, SUPPORT, PROBABILITY and VARIANCE may vary in meaning depending on their VALUETYPE. Fortunately, the possible values for VALUETYPE with Logistic Regression are all ones we’ve covered before, like the flags to indicate that columns are Missing, Existing, Continuous, Discrete, Discretized or represent parts of a regression equation, such as a coefficient. The sheer variety of node types makes the raw output of Logistic Regression more difficult to comprehend than that of previous algorithms though. We have a single marginal stats node, just like with Naïve Bayes, and one node for each predictable attribute directly under the model root, like with Decision Trees. Below that level, however, we must deal with nodes for the hidden layer (which is meaningless in Logistic Regression) and the output layer, as well as the output layer and its nodes. BOL contains an explanation of the numeric naming convention for the nodes which allows you to differentiate them by their function, but it is unwieldy unless you’ve written some DMX queries to turn them into human-readable labels.[vi]
The level of complexity ratchets up again when we move up to a full-blown neural net. Microsoft’s implementation of Logistic Regression is equivalent to its version of the Neural Network algorithm with its HIDDEN_NODE_RATIO parameter set at 0, which turns off the hidden layer of neurons. Even without that layer, Logistic Regression turned up some interesting results, including some relationships between Discrete columns like CounterID and WaitTypeID with measures of IO stress that could be quite revealing. For example, MaxWaitTimeMS is associated with several specific IO addresses and file identifiers when compared against a WaitTypeID we’ve assigned an ID value of 194 to, which corresponds to the wait type PREEMPTIVE_COM_DELETEROWS. I am not familiar with how IO subsystems work yet – which is one of the reasons I chose to poll this type of data for these mining tutorials – but I would assume that means certain wait intervals were associated with delete operations in certain database files, all of which can be looked up.
The specific General Statistics performance counter SQL Trace IO Provider Lock Waits and the counters Data File(s) Size (KB), Log File(s) Size (KB), Log File(s) Used Size (KB), Log Growths, Percent Log Used and Log Growths for all databases correlated very closely to certain WaitTypeIDs like QUERY_EXECUTION_INDEX_SORT_EVENT_OPEN, HADR_FILESTREAM_MANAGER and DBMIRROR_SEND in the context of high SignalWaitTimeMS values. The relationships between transaction log stress and increased wait times is exactly what we’d expect, although it would probably take a SQL internal guru to interpret the wait stats. The third mining structure has many Discrete inputs like QueryHashID, QueryPlanHashID, QueryTextID, SQLHandleID, PlanHandleID which we can correlate with specific queries and in many cases, specific values for them were strongly correlated to very high and very low values for important measures like IOStall.
In fact, Logistic Regression turned up so many potentially useful results that it would be beside the point to list them all here. The performance of the algorithm was also outstanding, to the point that we were able to turn off MAXIMUM_STATES without much sacrifice in terms of either processing time or the usefulness of the results. One of the trade-offs, at least in this particular trial, was in the form of results so numerous and potentially useful that we don’t have time to discuss them all – which is a rare form of information glut, instead of the usual double whammy that comes from overfitting. The real trade-off with this algorithm and its much more powerful cousin, the Neural Network algorithm, is in terms of the complexity of the results. Each data mining algorithm has its strengths and weaknesses and in the case of these two algorithms, this seems to be the major drawback. The problem is even more pronounced when we use the Neural Network algorithm, which ranks along with Time Series among the heavyweights of Microsoft’s nine data mining methods. Neural nets have received a lot of hype from Hollywood and the press in the last few decades, but it is deserved: as I can attest from personal experience, we’ve barely scratched the surface of their potential. They are designed to be analogous to the structures of biological brains (albeit at a very crude level) so it is not surprising that interpreting neural nets from their inner statistics is as difficult as reading a man’s thoughts from a coroner’s report on his cerebellum. The more powerful and useful a neural net is, the more this intrinsic dilemma comes to the fore. As we shall see in the next installment of this amateur blog, that is a small price to pay for one of the most exciting innovations in the history of data mining.
When I think of it being used for outcome-based predictions, what I picture is Young’s Double-Slit Interferometer, but that is a lot harder to visualize than an S-curve on a scatter plot without some introduction to quantum mechanics.
[ii] The first three are cited in the Wikipedia article “Logistic Regression”: http://en.wikipedia.org/wiki/Logistic_regression. The final two are mentioned in the BOL discussion on Logistic Regression.
[iii] For a longer, readable history of the algorithm, see Cramer, J.S., 2002, “The Origins of Logistic Regression.” A Tinburgen Institute discussion paper available online at http://www.tinbergen.nl/discussionpapers/02119.pdf. He doesn’t make any of the same criticisms of Malthusian logic that I do, but he does point out that the Club of Rome’s projections were off.
[iv] See he Wikipedia articles “Logistic Regression”: http://en.wikipedia.org/wiki/Logistic_regression and “Goodness of Fit” – http://en.wikipedia.org/wiki/Goodness_of_fit. For example, the latter refers to the Cox and Snell method and the Nagelkerke correction to it. Also see the MSDN webpage “Microsoft Logistic Regression Algorithm Technical Reference” at http://msdn.microsoft.com/en-us/library/cc645904.aspx
[v] See the MSDN webpage titled “Mining Model Content for Logistic Regression Models” at http://msdn.microsoft.com/en-us/library/cc645751.aspx
[vi] For an excellent explanation of what the lift figures mean, see the post by the user Josh Hemann on Oct. 17, 2011 at the Cross Validated webpage “Lift Measure in Data Mining” at http://stats.stackexchange.com/questions/17119/lift-measure-in-data-mining This website bills itself as “a collaboratively edited question and answer site for statisticians, data analysts, data miners and data visualization experts” and might serve as an excellent resource for anyone (such as myself) who needs a crash course in stats.