The Basics of Cryptology, Part 2

Introduction

In the first article of this series, we introduced the SQL Encryption Toolkit, which provides extended stored procedures for SQL Server 2000 to perform basic cryptographic functions using the Blowfish and AES encryption algorithms. In the second article, we discussed the history of cryptography and the basics of modern cryptography.

In this, the third and final installment, we will take a look at the how a modern cryptographic algorithm does its job. This article will provide a basic overview of the mathematical theory behind modern encryption, and it will provide links to detailed documents that describe the precise mathematical models and functions used.

A "Bit" About Math and Logic

A bit is the smallest unit of data that modern computers can operate on. Cryptographic input is viewed by the cryptographic algorithm as blocks (or streams, in some instances) of bits. The algorithm's job is to scramble the input bits sufficiently to make them unrecoverable until they are run through the decryption process with a proper decryption key.

The cryptographer's toolkit includes basic math operators, logical operators and other bit-level operators and their inverse operators. As mentioned in the previous article, Addition (+) is the inverse of Subtraction (-). What this means is if we add any number y to any number x, we can recover the original value of x by performing the inverse operation with y.

Figure 1. Addition and Subtraction Operators

Likewise, Multiplication (*) is the inverse of Division(/).

In addition to the basic math operators above, the Exclusive OR logical operator () (commonly abbreviated "XOR", "EXOR" or "EOR") is often used in cryptography. XOR is formally defined as the "bit-wise exclusive disjunction operator." In plain English, this means that any two bits that are XOR'd together, will result in "1" if, and only if, one of the two bits is a "1." If both bits are "0" or both bits are "1", the result of XOR is "0."

XOR is quite useful in cryptography for another reason. It just happens to be its own inverse. As an example, say we are given the hexadecimal number 0xF0, and we perform an XOR with 0xCC. We’ll demonstrate the operation with bits:

Figure 2. XOR Operation.

To get our original value back, we simply XOR the result of the previous XOR operation with 0xCC again:

Figure 3. Reversing an XOR operation.

Because of this property, XOR is extremely useful in obscuring and recovering our plain text.

Another set of operations commonly used in encryption are the bit shift operators. The bit shift family of operators includes the "shift left" and "shift right" operations, which shift a row of bits to the right or left:

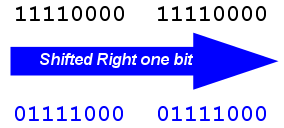
Figure 4. Right-shifting a row of bits.

Putting it all together we can turn our plain text into a nicely jumbled, but easily reversible, mess. However, with just our plain text, encryption key and these operators we still haven't eliminated patterns from our encrypted text. These patterns that occur are the basis of "codebook attacks" and other reverse-engineering methods. So how do we get rid of patterns in our encrypted data?

State of Confusion

In the last article we looked at the distribution of letters in written English. Because some letters occur more frequently than others, several methods have been developed to reverse-engineer the output of simple ciphers.

Substitution Boxes, or S-Boxes as they are commonly known, are arrays of bytes that obscure the relationship between our plain text and our encrypted text via simple substitutions. S-Boxes perform a function known as "confusion."

Figure 5. Confusion Operation

The S-Box confusion operation in the example simply substitutes our 8 bits with another set of 8 bits from the S-Box lookup table. But just replacing all occurrences of one byte with another byte still leaves the frequency of occurrence clearly visible to cryptanalysts out there.

To handle the frequency of occurrence problem, we turn to "diffusion." Diffusion is a method designed to eliminate statistical patterns from our input data. Some cryptographic algorithms like DES use Permutation Boxes, or P-Boxes, to re-order bits during encryption. Other algorithms, like AES, perform row-shifting and column-mixing steps to provide diffusion.

Figure 6. Diffusion Operations

The essence of diffusion is that a cryptanalyst will not be able to count the number of occurrences of a byte/character and determine that he should replace that byte with “E”. Because of diffusion, the encrypted form of "E" will have the same probability of occurrence as the encrypted form of "Z." Diffusion makes it more difficult to reverse engineer mathematical patterns from our encrypted text.

Mix Well

So, to put it all together, we end up with an encryption algorithm like the Advanced Encryption Standard (AES/Rijndael). Here is an AES sample that demonstrates the end result of all this knowledge:

Figure 7. Encryption Sample, Plain Text

Since AES encrypts blocks of 16 bytes, our algorithm automatically pads the plain text with 11 bytes. Per FIPS padding specifications, we pad with 10 zeroes plus the count of padding characters (10) in the last byte. Here is our encrypted message:

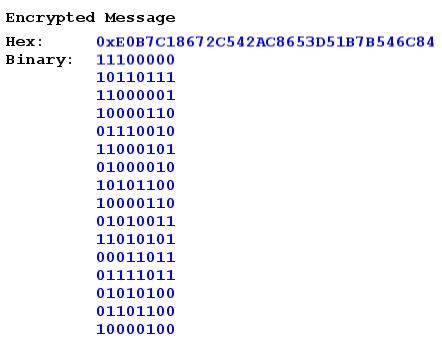
Figure 8. Encryption Sample, Encrypted Text

As can be seen, the original message, "TEST!" has now been thoroughly encrypted by the AES algorithm. Notice that, even though the 6^th through the 15^th bytes are nothing more than a string of zeroes, thanks to diffusion, there is no discernable pattern that would clue a cryptanalyst in to this fact.

Conclusion

This is the final part of a three part series on Cryptography. In this article we touched on the inner workings of cryptographic algorithms and the operations that make it all possible.

AES and Blowfish Encryption are both available in the SQL Encryption Toolkit.

Resferences

• Wikipedia. Advanced Encryption Standard (AES). http://en.wikipedia.org/wiki/Rijndael_encryption_algorithm
• Shannon, C.E. Communication Theory of Secrecy Systems. http://www.cs.ucla.edu/~jkong/research/security/shannon1949.pdf
• Wikipedia. Blowfish (cipher). http://en.wikipedia.org/wiki/Blowfish_%28cipher%29
• Daeman and Rijmen. AES Proposal. - https://csrc.nist.gov/csrc/media/projects/cryptographic-standards-and-guidelines/documents/aes-development/rijndael-ammended.pdf
• Coles, M. SQL Encryption Toolkit. http://www.sqlservercentral.com/columnists/mcoles/freeencryption.asp