This is the first article in a short series of SQL Server query challenges to test and expand your SQL Server querying skills. While none of these short articles is of overwhelming complexity, they will hopefully either teach you something new or help you to reactivate potentially dormant SQL skills in preparation for your next real-world challenge. You can see the rest of the articles on the Query Answers with SQL Server page.

In this article we will imagine that you are working for a small classic car retailer, called Prestige Cars Ltd, using the data that is in the company database.

The Challenge

“Money is expensive” is a frequently recurring mantra in most businesses. So, imagine that the CFO of Prestige Cars has devoted countless hours to developing spreadsheets that count the cost of unsold stock in the showroom. Now, unfortunately, he wants you to adapt his basic compound interest calculation to SQL so that your reports can show how much “dead metal” (to use the term the CFO uses to describe unsold stock) actually costs the company.

To help you in your work he has added that:

• You are to use a standard compound interest calculation.
• The interest is to be compounded monthly.
• The rate that he wants to apply is 0.75 percent per month.
• You are only to calculate interest when a vehicle is in stock for over two months.

As a further hint, he has kindly emailed you the exact calculation that he wants you to apply. This is the one in Figure 1 below.

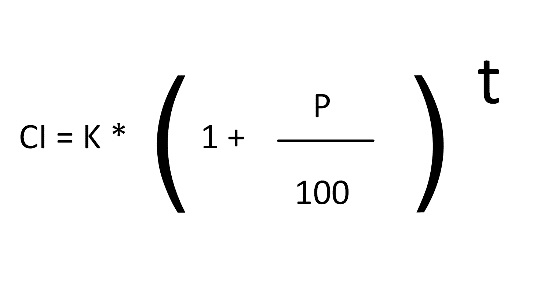
Figure 1. A compound interest calculation

Your challenge is to come up with the SQL that shows not only the interest charge, but also the number of months since the vehicle was purchased as well as the cost price and the total cost including interest.

Using the sample data for this article (the “PrestigeCars” database in the Resources section) this is the kind of SQL that you could write to answer the requirement:.

SELECT InitialCost,
       MonthsSincePurchase,
       (InitialCost * POWER(1 + (0.75 / 100), MonthsSincePurchase)) - InitialCost AS InterestCharge,
       InitialCost * POWER(1 + (0.75 / 100), MonthsSincePurchase) AS TotalWithInterest
FROM
(
    SELECT DATEDIFF(mm, DateBought, SL.SaleDate) AS MonthsSincePurchase,
           (Cost + PartsCost + RepairsCost) AS InitialCost
    FROM Data.Stock SK
        INNER JOIN Data.SalesDetails SD
            ON SK.StockCode = SD.StockID
        INNER JOIN Data.Sales SL
            ON SL.SalesID = SD.SalesID
    WHERE DATEDIFF(mm, DateBought, SL.SaleDate) > 2
) SRC;

Running this code snippet gives the result that you can see in Figure 2.

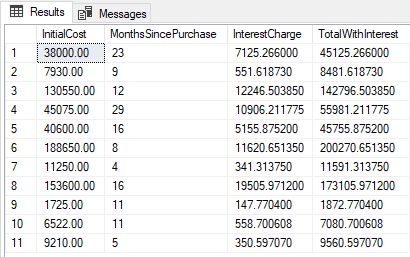
Figure 2. Calculating compound interest

How It Works

Creating complex calculations in SQL is a vast subject. Indeed, entire books and papers have been written on this subject. So, although we want to show you the basics of using SQL to handle intricate financial mathematics, we are not delving too profoundly into this subject.

Given that this challenge could be complex, we have started by breaking it down into two parts.

An inner query

That calculates the total cost of a vehicle by adding up the purchase cost, cost of spares, and any repair costs. This query then also determines the number of months between the purchase date and the sale date.

An outer query

The outer query displays the two fields isolated by the inner query (InitialCost and MonthsSincePurchase). The outer query then uses these two fields as core elements in calculating the compound interest.

What is both interesting and new in this query is the compound interest calculation, so now you need to look at this in more detail. Essentially you have applied a two-step process to calculating compound interest:

In the first part, you take the arithmetical formula and adapt it so that it can be read on a single line.

The second part is convering the single-line formula to SQL. Converting the formula from Figure 1 to a single line gives you the following:

CI = K * (1 + P/100)t

where

• CI is the compound interest (including the original capital value)
• K is the initial value
• P is the interest rate
• t is the number of periods

The SQL that delivers the compound interest (CI) takes the initial value (K) to be the purchase cost, cost of spares, and any repair costs. It then “hard-codes” the interest rate as 0.75 and divides by 100 to express it as a percentage. Finally it uses the POWER() function to apply the number of periods (t) as the exponent for the formula. The number of periods is, in fact, the number of months between purchase and sale. 

The POWER() function takes two parameters. The first parameter is the base value you wish to raise to the power of the exponent (one plus the percentage interest rate in this example). The second parameter is the exponent to apply (the number of months in this example).

As a final tweak, this calculation is applied a second time. Only on this occasion, the initial cost is subtracted from the compound interest to leave the actual interest amount. This way you can see the total cost as well as the interest.

This is, of course, only a simple example. Financial calculations can get much more complicated than this one. However, it is a starting point on which you can build to develop much more complex analyses if you need to.

Of course, you need to understand the PrestigeCars database if you are going to comprehend this code – especially the FROM/JOIN clauses. To make your life easier, here is the ERD (Entity Relationship Diagram) for this database:

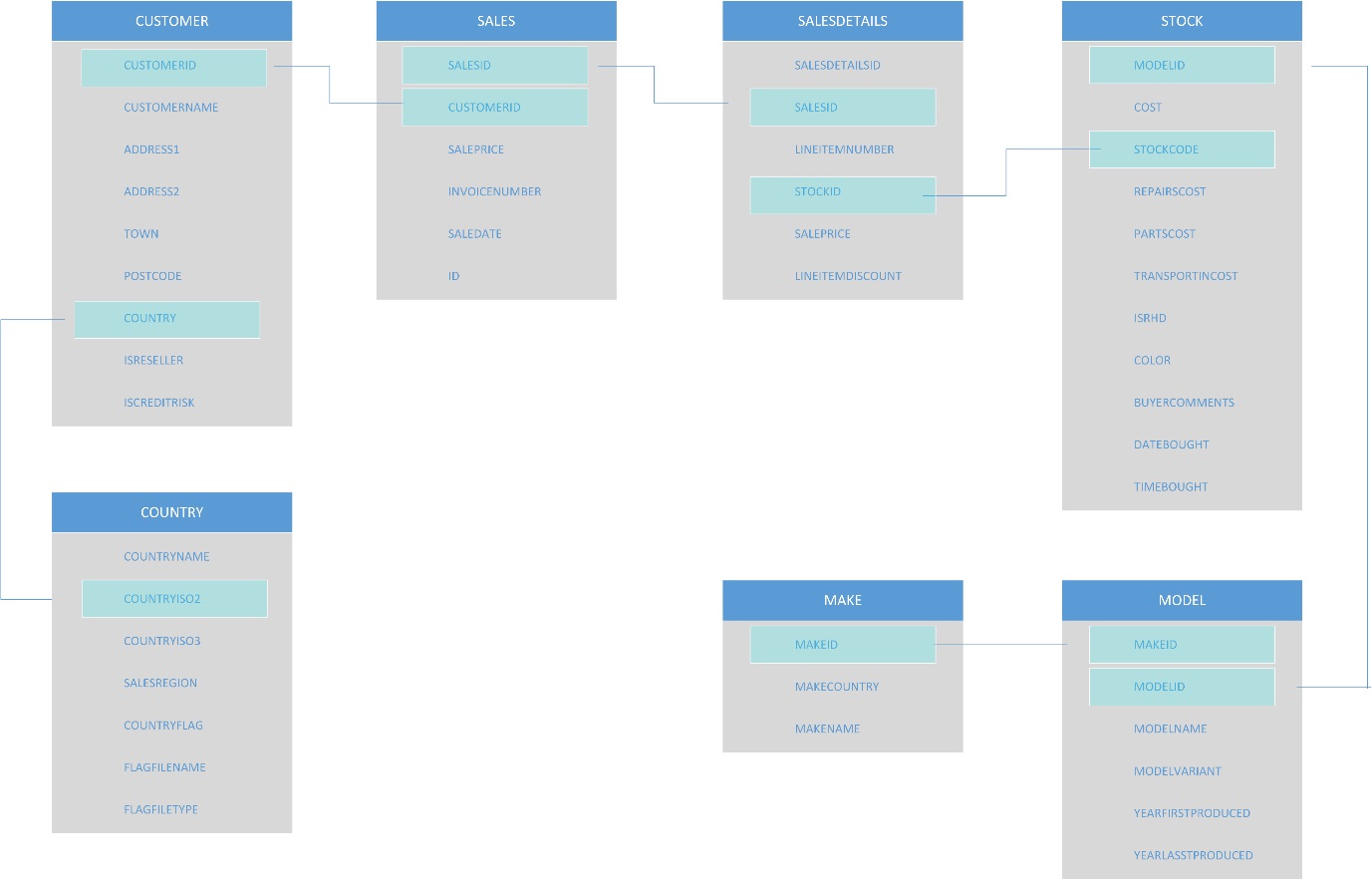
Figure 3: The Prestige Cars database Entity Relationship Diagram

Tricks and Traps

There are a few ideas that you can take away from this example. First, it is possible to write a query like this one without actually using a subquery; however, we feel that the improved simplification and increased clarity that a subquery brings to both the analysis and the coding make a subquery worth any extra effort. More complex financial or mathematical formulas can be translated into SQL using this approach. Essentially this means restructuring the formula so that it can be represented as a single line, then converting the arithmetic to SQL.

That is it – you have seen a simple example of how to port a compound interest calculation to T-SQL. Keep watching SQL Server Central.com ready for the next article in this series.

This article is adapted from the book “Query Answers with SQL Server Volume II: In-Depth Querying” by Adam and Karine Aspin. Available as both a paperback and an eBook from all good resellers including Amazon, Kobo and iBooks, as well as all good bookstores.

The sample data is available either in the accompanying material for this article, or on the Tetras Publishing website at: www.tetraspublishing.com/sqlserver.

The Series

There are a number of articles in this series. You can see them all on the Query Answers page.