Problem
Finding the hole for continuous sequences of numbers could be a discouraging task even for advanced programmers. This article presents a new solution based on usage of geometry data type and on a unknown function (if not, maybe less used function) specific designed for geometry objects.
Sample: Given the following sequence of [dis]continuous numbers 1, 2, 7, 8, 9, 10, 30 how to compute the missing intervals [3, 6], [11, 29] ?
Proposed Solution
The first step in combining these integers into ranges suppose the transformation of every integer into range [Integer-1, Integer] and then into a spatial polygon thus:
POLYGON((Integer 0),(Integer 1),(Integer-1 1),(Integer-1 0),(Integer 0)).
For example 30 become following object
POLYGON((30 0, 30 1, 29 1, 29 0, 30 0))
Full interval list:
DECLARE @tab TABLE(Col1 GEOMETRY);
INSERT @tab(Col1)
SELECT GEOMETRY::STGeomFromText('POLYGON((1 0, 1 1, 0 1, 0 0, 1 0))', 0) -- 1
UNION ALL
SELECT GEOMETRY::STGeomFromText('POLYGON((2 0, 2 1, 1 1, 1 0, 2 0))', 0) -- 2
UNION ALL
SELECT GEOMETRY::STGeomFromText('POLYGON((7 0, 7 1, 6 1, 6 0, 7 0))', 0) -- 7
UNION ALL
SELECT GEOMETRY::STGeomFromText('POLYGON((8 0, 8 1, 7 1, 7 0, 8 0))', 0) -- 8
UNION ALL
SELECT GEOMETRY::STGeomFromText('POLYGON((9 0, 9 1, 8 1, 8 0, 9 0))', 0) -- 9
UNION ALL
SELECT GEOMETRY::STGeomFromText('POLYGON((10 0, 10 1, 9 1, 9 0, 10 0))', 0) -- 10
UNION ALL
SELECT GEOMETRY::STGeomFromText('POLYGON((30 0, 30 1, 29 1, 29 0, 30 0))', 0); -- 30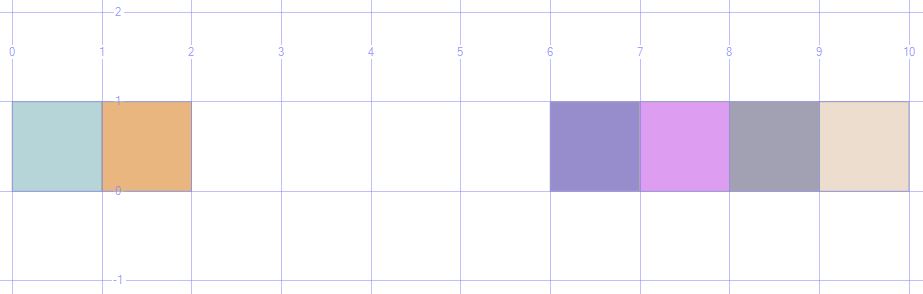
Next step of this new solution suppose the merge of these integers into intervals of continuous values using the UnionAggregate function. The end results is a MULTIPOLYGON spatial geometry object (having intermediary points):
DECLARE @pol GEOMETRY; DECLARE @ranges GEOMETRY; SELECT @pol = GEOMETRY::UnionAggregate(t.Col1) FROM @tab t; SELECT @pol, @pol.STAsText(); The end result:
MULTIPOLYGON ( ((29 0, 30 0, 30 1, 29 1, 29 0)), ((6 0, 7 0, 8 0, 9 0, 10 0, 10 1, 9 1, 8 1, 7 1, 6 1, 6 0)), ((0 0, 1 0, 2 0, 2 1, 1 1, 0 1, 0 0)) )
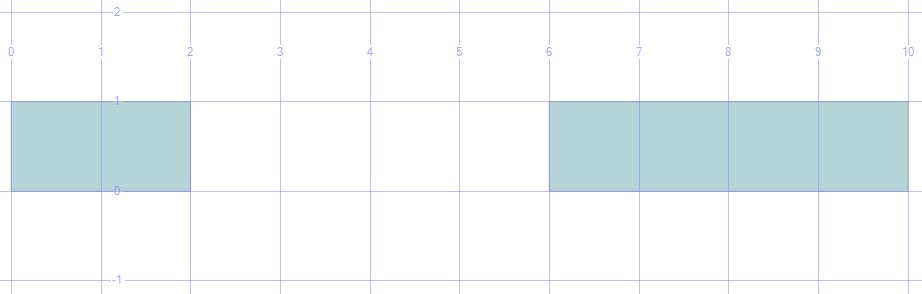
The final step is to generate the envelope (the bounding box) for these polygons using
@pol.STEnvelope() -- POLYGON ((0 0, 30 0, 30 1, 0 1, 0 0))
and then to compute the difference between envelope
POLYGON ((0 0, 30 0, 30 1, 0 1, 0 0))
and combined intervals
MULTIPOLYGON ( ((29 0, 30 0, 30 1, 29 1, 29 0)), ((6 0, 7 0, 8 0, 9 0, 10 0, 10 1, 9 1, 8 1, 7 1, 6 1, 6 0)), ((0 0, 1 0, 2 0, 2 1, 1 1, 0 1, 0 0)) ) using the STSymDifference() function like this:
SELECT @ranges = @pol.STEnvelope().STSymDifference(@pol);
SELECT @ranges, @ranges.STAsText();
The result of STSymDifference() is a MULTIPOLYGON object containing the missing polygons from envelop:
MULTIPOLYGON ( ((10 0, 29 0, 29 1, 10 1, 10 0)), ((2 0, 6 0, 6 1, 2 1, 2 0)) )
Source Code
The final source code is:
DECLARE @tab TABLE(Col1 GEOMETRY);
INSERT @tab(Col1)
SELECT GEOMETRY::STGeomFromText('POLYGON((1 0, 1 1, 0 1, 0 0, 1 0))', 0) -- 1
UNION ALL
SELECT GEOMETRY::STGeomFromText('POLYGON((2 0, 2 1, 1 1, 1 0, 2 0))', 0) -- 2
UNION ALL
SELECT GEOMETRY::STGeomFromText('POLYGON((7 0, 7 1, 6 1, 6 0, 7 0))', 0) -- 7
UNION ALL
SELECT GEOMETRY::STGeomFromText('POLYGON((8 0, 8 1, 7 1, 7 0, 8 0))', 0) -- 8
UNION ALL
SELECT GEOMETRY::STGeomFromText('POLYGON((9 0, 9 1, 8 1, 8 0, 9 0))', 0) -- 9
UNION ALL
SELECT GEOMETRY::STGeomFromText('POLYGON((10 0, 10 1, 9 1, 9 0, 10 0))', 0) -- 10
UNION ALL
SELECT GEOMETRY::STGeomFromText('POLYGON((30 0, 30 1, 29 1, 29 0, 30 0))', 0); -- 30
DECLARE @pol GEOMETRY;
DECLARE @ranges GEOMETRY;
SELECT @pol = GEOMETRY::UnionAggregate(t.Col1)
FROM @tab t;
SELECT @pol, @pol.STAsText();
SELECT @ranges = @pol.STEnvelope().STSymDifference(@pol);
SELECT @ranges, @ranges.STAsText();
SELECT
Range_N = val.number,
Range_Polygon= @ranges.STGeometryN(val.number).STEnvelope().ToString(),
Range_Start = @ranges.STGeometryN(val.number).STEnvelope().STPointN(1).STX+1,
Range_End = @ranges.STGeometryN(val.number).STEnvelope().STPointN(2).STX
FROM master.dbo.spt_values val
WHERE val.type = N'P'
AND val.number >= 1
AND val.number <= @ranges.STNumGeometries();
Final Conclusions
This article describe a brand new solution for the problem of finding the missing intervals for sequences of continuous integers using spatial objects: POLYGON, MULTIPOLYGON and functions: UnionAggregate(), STEnevelope(), STSymDifference(), STNumGeometries(), STGeometryN().
Note: Please read also this article https://www.sqlservercentral.com/articles/collections


