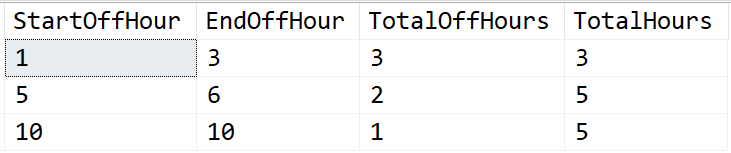Gap Analysis Using Algebra
-
March 10, 2020 at 12:00 am
Comments posted to this topic are about the item Gap Analysis Using Algebra
-
March 10, 2020 at 12:27 pm
First, thank you for the article. I think that anyone that steps up to the plate to share their knowledge is ok in my book.
Shifiting gears, I'm a bit confused by the claim in the Introduction, which states... (and the emphasis is mine)
Introduction
This article shows how to solve a gaps and islands problem using simple algebra. No SQL Server loops or cursors are required for this solution.
And then we look at the code for both fnBasic and fnConstraint and see that, clearly, they both contain a WHILE loop not to mention the fact that they're Scalar Functions, which is not inline code (prior to 2019) and creates a form of hidden RBAR that's frequently worse than a WHILE loop.
And so I'm curious how you thought the claim of "No SQL Server loops or cursors are required for this solution" was anywhere near the truth.
--Jeff Moden
RBAR is pronounced "ree-bar" and is a "Modenism" for Row-By-Agonizing-Row.
First step towards the paradigm shift of writing Set Based code:
________Stop thinking about what you want to do to a ROW... think, instead, of what you want to do to a COLUMN.Change is inevitable... Change for the better is not.
Helpful Links:
How to post code problems
How to Post Performance Problems
Create a Tally Function (fnTally) -
March 10, 2020 at 1:44 pm
You are absolutely right.
The main point to this article is that the definition of basic sets paved the way for an algebraic solution, which surprised me.
-
March 10, 2020 at 2:48 pm
Ok... "Basic Sets". Let's do that. I don't have time just now to write the full solution (on my way to work, which also means that it's not fully tested) but consider what you might be able to do with the results of the following (this code would be the basis for a high performance iTVF)...
DECLARE @Periods VARCHAR(720) = '0001001110' --Original string from example in article
;
WITH cteGroup AS
(--==== Subtract the running total of off hours from an enumeration of hours to form "off hour groupings".
SELECT Hr = t.N
,IsOff = ABS(CONVERT(INT,SUBSTRING(@Periods,t.N,1))-1)
,Grp = t.N-SUM(ABS(CONVERT(INT,SUBSTRING(@Periods,t.N,1))-1)) OVER (ORDER BY t.N)
FROM dbo.fnTally(1,LEN(@Periods)) t
)
,cteTotalOffHours AS
(--==== If we find the Min and the Max of each off hour grouping, we end up with the start and end hour of each grouping.
SELECT StartOffHour = MIN(Hr)
,EndOffHour = MAX(Hr)
,TotalOffHours= MAX(Hr)-MIN(Hr)+1
FROM cteGroup
WHERE IsOff = 1
GROUP BY Grp
)
SELECT * --Total Hours is the number of hours of both time on and off since the beginning of the previous time off grouping
,TotalHours = EndOffHour-StartOffHour
+ (StartOffHour-LAG(StartOffHour,1,0) OVER (ORDER BY StartOffHour))
FROM cteTotalOffHours
;... and that provides the following result.
See the link for the code for the fnTally function in my signature line below, which is also a "basic set" formed by a "Psuedo-Cursor" in the form of a cCTE (Cascading CTE) (thank you Itzik Ben-Gan), which must not be confused with a slothful, resource intensive rCTE (Recursive CTE).
--Jeff Moden
RBAR is pronounced "ree-bar" and is a "Modenism" for Row-By-Agonizing-Row.
First step towards the paradigm shift of writing Set Based code:
________Stop thinking about what you want to do to a ROW... think, instead, of what you want to do to a COLUMN.Change is inevitable... Change for the better is not.
Helpful Links:
How to post code problems
How to Post Performance Problems
Create a Tally Function (fnTally) -
March 10, 2020 at 4:40 pm
Thank you Jeff for a more elegant computation of fnBasic.
-
March 12, 2020 at 3:02 am
A SQL Server solution to this problem, without using mathematics, would be very interesting. This was a real problem that I worked on, and I expected to do some fancy C++ footwork on arrays to compute the constraint function. However, when I finally realized that only basic sets were required in any computation, I began to see how the distances between them determine non-compliance of the function. That's when the algebra kicked in. But if this could be done with pure SQL, that would be impressive.
-
March 12, 2020 at 4:41 am
Glen Cooper wrote:A SQL Server solution to this problem, without using mathematics, would be very interesting. This was a real problem that I worked on, and I expected to do some fancy C++ footwork on arrays to compute the constraint function. However, when I finally realized that only basic sets were required in any computation, I began to see how the distances between them determine non-compliance of the function. That's when the algebra kicked in. But if this could be done with pure SQL, that would be impressive.
So far, I've only used T-SQL but, even with that, there are some basic mathematics involved like the trick with determining groups by subtraction from a sequence. Even SQL itself is based on relational algebra. So what to you mean by "done with pure SQL"? If you mean with no mathematics, I'll be the first to say that it can't be done.
The code basis that I've demonstrated so far provides a pretty good base to work from if you consider the off hours vs the total hours, the latter of which is based on the number of hours between the start of any off hour group. If you have no 24's showing up in the off hours, case closed... it's a violation. If you sequester only the rows where the total number of off hours is >= 24 and measure the distance between those rows (using LEAD or LAG) and that distance exceeds the number of hours in a week, you have another violation.
I've got a pretty full dance card for the rest of the week but I'll try to gin up some test data that closer to the problem you described and see if my proposed solution works... I'll do it for a 5 year period just to make sure that 1) it works and 2) the performance is good.
The key is just like you said... basic sets. The only difference between what you did for the basic function and what I did is how those basic sets were derived. I just did what you did in a different manner.
And, yes... it IS an interesting problem.
--Jeff Moden
RBAR is pronounced "ree-bar" and is a "Modenism" for Row-By-Agonizing-Row.
First step towards the paradigm shift of writing Set Based code:
________Stop thinking about what you want to do to a ROW... think, instead, of what you want to do to a COLUMN.Change is inevitable... Change for the better is not.
Helpful Links:
How to post code problems
How to Post Performance Problems
Create a Tally Function (fnTally) -
March 12, 2020 at 11:52 am
By "using mathematics" I meant "proving a new mathematical theorem or quoting on old one".
I had to prove a theorem to write this script.
I'm wondering aloud how a functionally equivalent SQL Server script could be written where you didn't have to prove a theorem or quote and old one.
-
March 12, 2020 at 2:30 pm
Ah... gotcha. Thanks, Glenn. I'll do my best over the weekend.
--Jeff Moden
RBAR is pronounced "ree-bar" and is a "Modenism" for Row-By-Agonizing-Row.
First step towards the paradigm shift of writing Set Based code:
________Stop thinking about what you want to do to a ROW... think, instead, of what you want to do to a COLUMN.Change is inevitable... Change for the better is not.
Helpful Links:
How to post code problems
How to Post Performance Problems
Create a Tally Function (fnTally)
Viewing 9 posts - 1 through 9 (of 9 total)
You must be logged in to reply to this topic. Login to reply