At first glance, the question of how many rows are estimated from a table variable is easy.
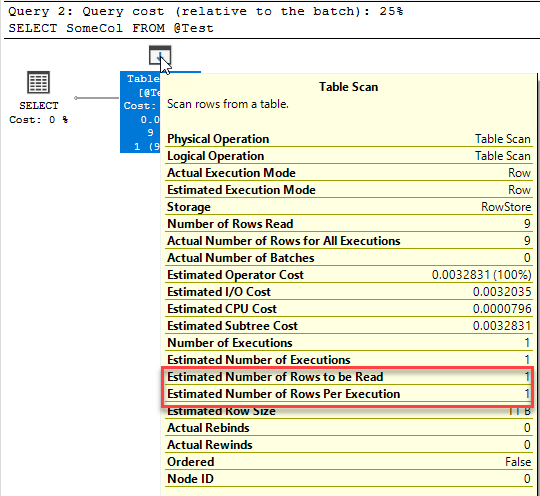
But, is it really that simple? Well, not really. To dig into the why, first we need to identify why table variables estimate 1 row. The obvious answer is because they don’t have statistics. However…
ALTER DATABASE CURRENT SET AUTO_CREATE_STATISTICS OFF
GO
CREATE TABLE Test (SomeCol INT);
INSERT INTO Test (SomeCol)
VALUES (1),(22),(37),(45),(55),(67),(72),(86),(91)
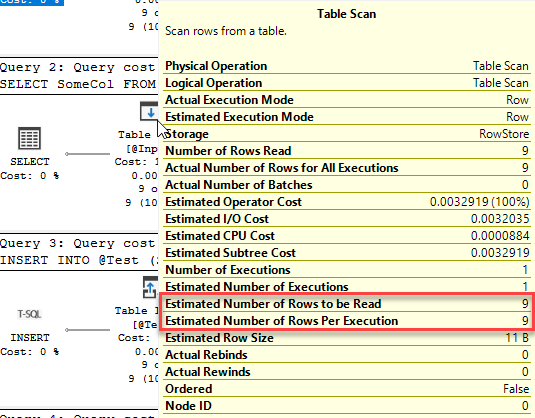
SELECT SomeCol FROM Test
SELECT * FROM sys.stats WHERE object_id = OBJECT_ID('Test')
DROP TABLE dbo.Test
That table has no statistics, but it still estimates rows correctly.

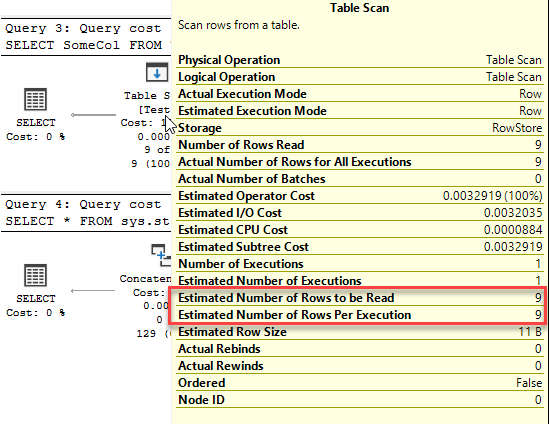
So it’s not just the absence of statistics. Hmmm… Where else is there a difference with a table variable?
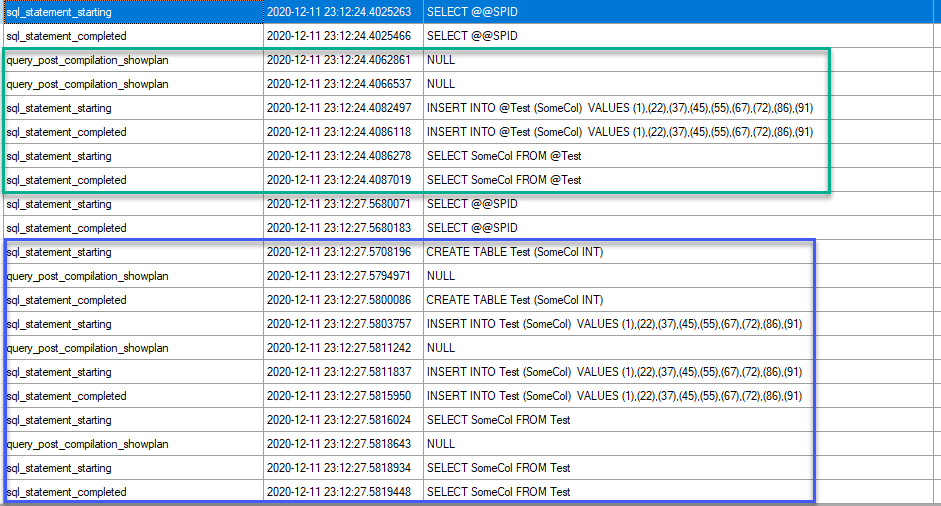
It has to do with when the plans are generated. The XE event results are from an event tracking statement start and end and the post-compilation event for the plan. For the query using the table variable, the entire batch is compiled before the execution starts. For the permanent table, there are multiple compilation events.
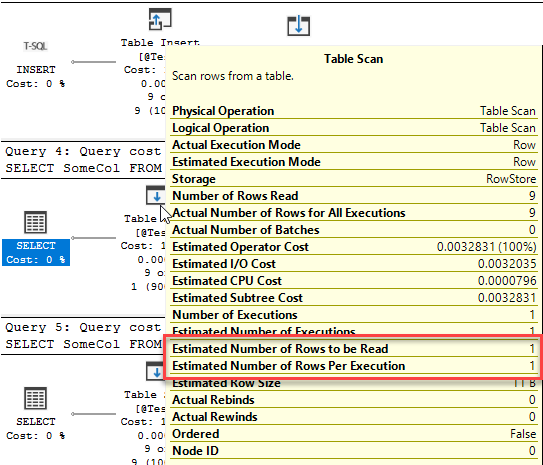
And this is because of something called ‘deferred compile’. For the table variable, the entire batch is compiled at the start, at a time where the table variable does not exist, and because there are no statistics, no recompile is triggered after the insert. Hence, there cannot be any row estimation other than 1 row, because the table did not exist when the estimate was made.
For the permanent table, the compilation of the query that uses the table is deferred until the query starts, not when the batch starts. Hence the plan for the query is generated after the table exists, after it’s been populated. That’s the difference here.
Now, there’s still no statistics, and so there’s no way to get data distribution, but that’s not the only way to get information on the rows in the table. The Storage Engine knows how many rows are in the table, though data distribution isn’t known.
Hence, with a table variable we can expect to see an estimated row count other than 1 any time the table variable exists before the query that uses it is compiled.
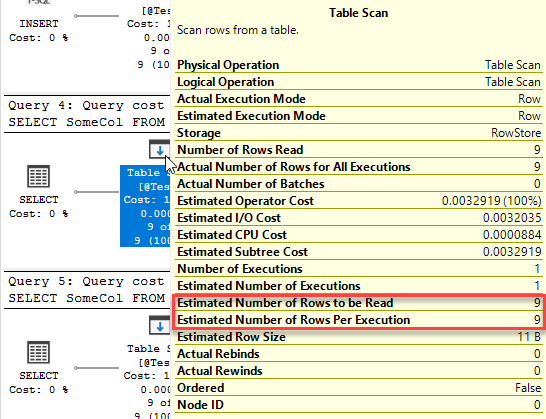
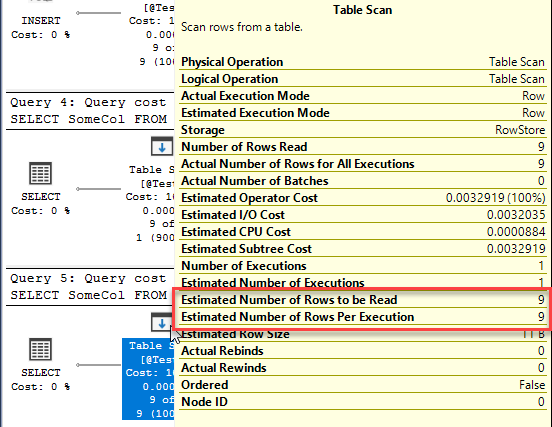
That will happen when the table variable is a table-type parameter, when the query using it has the RECOMPILE option, and when SQL 2019’s deferred compile for table variables is in play.
CREATE OR ALTER PROCEDURE TestRowEstimations @Input TestTableType READONLY AS SELECT SomeCol FROM @Input; DECLARE @Test TABLE (SomeCol INT); INSERT INTO @Test (SomeCol) VALUES (1),(22),(37),(45),(55),(67),(72),(86),(91); SELECT SomeCol FROM @Test; SELECT SomeCol FROM @Test OPTION (RECOMPILE); GO